Question

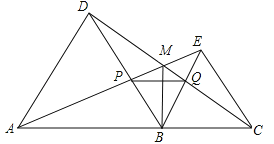
【题目】如图，点A，B，C在一条直线上，△ABD，△BCE均为等边三角形，连接AE和CD，AE分别交CD，BD于点M，P，CD交BE于点Q，连接PQ，BM，下面结论：①△ABE≌△DBC；②∠DMA=60°；③△BPQ为等边三角形；④MB平分∠AMC，

其中结论正确的有（ ）

A．1个 B．2个 C．3个 D．4个

Answer 1

【答案】D．

【解析】

试题分析：∵△ABD、△BCE为等边三角形，∴AB=DB，∠ABD=∠CBE=60°，BE=BC，∴∠ABE=∠DBC，∠PBQ=60°，在△ABE和△DBC中，∵AB=DB，∠ABE=∠DBC，BE=BC，∴△ABE≌△DBC（SAS），∴①正确；

∵△ABE≌△DBC，∴∠BAE=∠BDC，∵∠BDC+∠BCD=180°﹣60°﹣60°=60°，∴∠DMA=∠BAE+∠BCD=∠BDC+∠BCD=60°，∴②正确；

在△ABP和△DBQ中，∵∠BAP=∠BDQ，AB=DB，∠ABP=∠ADBQ=60°，∴△ABP≌△DBQ（ASA），∴BP=BQ，∴△BPQ为等边三角形，∴③正确；

∵∠DMA=60°，∴∠AMC=120°，∴∠AMC+∠PBQ=180°，∴P、B、Q、M四点共圆，∵BP=BQ，∴，∴∠BMP=∠BMQ，即MB平分∠AMC，∴④正确；

综上所述：正确的结论有4个，故选D．