题目内容
【题目】如图,两直线AB,CD相交于点O,已知OE平分∠BOD,且∠AOC:∠AOD=3:7,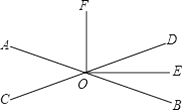
(1)求∠DOE的度数;
(2)若OF⊥OE,求∠COF的度数.
【答案】
(1)解:∵两直线AB,CD相交于点O,∠AOC:∠AOD=3:7,
∴∠AOC=180°× ![]() =54°,
=54°,
∴∠BOD=54°,
又∵OE平分∠BOD,
∴∠DOE=54°÷2=27°;
(2)解:∵OF⊥OE,∠DOE=27°,
∴∠DOF=63°,
∠COF=180°-63°=117°.
【解析】(1)根据平角的定义和∠AOC:∠AOD=3:7,可求出∠AOC的度数,再由对顶角相等可得∠BOD的度数,然后由角平分线的定义可求出∠DOE的度数;
(2)OF⊥OE,可得∠EOF=90° ,进而可求出∠DOF的度数,再由∠COF+∠DOF=180°可求出∠COF的度数.
【考点精析】本题主要考查了角的平分线和角的运算的相关知识点,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;角之间可以进行加减运算;一个角可以用其他角的和或差来表示才能正确解答此题.

练习册系列答案
相关题目