题目内容
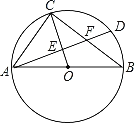
【题目】如图,![]() 是⊙
是⊙![]() 的直径,
的直径,![]() 为⊙
为⊙![]() 的弦,
的弦,![]() ⊥
⊥![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,过
,过![]() 点的直线交
点的直线交![]() 于点
于点![]() ,且∠
,且∠![]() =∠
=∠![]() .
.
(1)求证:![]() 为⊙
为⊙![]() 的切线;
的切线;
(2)若![]() =2,
=2,![]() =
=![]() ,则线段
,则线段![]() 的长为 .
的长为 .
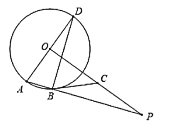
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OB,如图,根据圆周角定理得到∠ABD=90°,再根据等腰三角形的性质和已知条件证出∠OBC=90°,即可得出结论;
(2)证明△AOP∽△ABD,然后利用相似比求BP的长.
(1)证明:连结![]() .
.
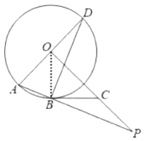
∵![]() 为
为![]() 直径,
直径,![]() 为
为![]() 的弦,
的弦,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∵![]() 为
为![]() 半径,
半径,
∴![]() 为
为![]() 切线.
切线.
(2)∵OA=2,
∴AD=2OA=4,
∵OP⊥AD,
∴∠POA=90°,
∴∠P+∠A=90°,
∴∠P=∠D,
∵∠A=∠A,
∴△AOP∽△ABD,
∴![]() =
=![]() ,即
,即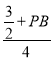 =
=![]() ,
,
解得:BP=![]() ,
,
故答案为:![]() .
.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
【题目】某商店购进一批成本为每件40元的商品,若商店按单价不低于成本价,且不高于70元销售,且销售单价为正整数,经调查发现,该商品每天的销售量y(件)与销售单价x(元)之间的关系如表:
销售单价x/元 | 40 | 50 | 60 | 70 |
每天的销售量y/件 | 140 | 120 | 100 | 80 |
(1)请你认真分析表中所给的数据,用你学过的一次函数、反比例函数和二次函数中的一种来表示y与x之间的变化规律,说明选择这种函数的理由,并求出它的函数表达式和自变量的取值范圈.
(2)销售单价定为多少元时,才能使销售该商品每天获得的利润最大?最大利润是多少元?