Question

【题目】如图，济南市为加快网络建设，某通信公司在一个坡度为的山腰上建了一座垂直于水平面的信号通信塔，在距山脚处水平距离的点处测得通信塔底处的仰角是，通信塔顶处的仰角是.则通信塔的高度为（ ）（结果保留整数，参考数据：，）

A.B.C.D.

Answer 1

【答案】C

【解析】

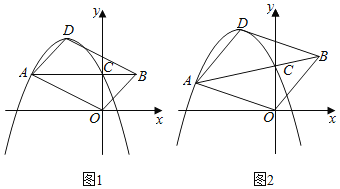
延长AB交DC延长线于点E，根据坡度的概念设CE=x，得到BE=2x，根据正切的概念列式求出x，得到DE的长，根据正切的定义求出AE，计算即可．

延长AB交DC延长线于点E，则AE⊥DC，

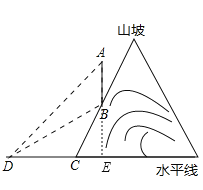
由题意知∠BDC=30°，∠ADE=45°，CD=24，

∵BC的坡度为2：1，

∴设CE=x、则BE=2x、DE=24+x，

在Rt△BDE中，，即，

解得：x=10，

∴DE=24+x=34，BE=2x=20，

在Rt△ADE中，AE=DEtan∠ADE≈34×1=34，

则AB=AE-BE=34-20=14，

答：通信塔AB的大约高度约为14米．

故选：C．