题目内容
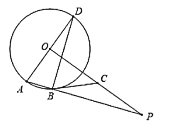
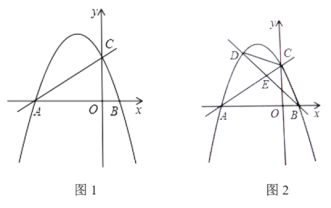
【题目】如图1,![]() 是
是![]() 的直径,
的直径,![]() 为
为![]() 上不同于
上不同于![]() 的两点,连接
的两点,连接![]() 且
且![]() 过点
过点![]() 作
作![]() 垂足为
垂足为![]() 直线
直线![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]()
①求直径![]() 的长;
的长;
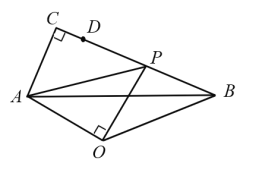
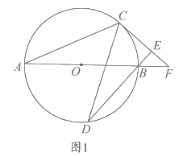
②如图2所示,连接![]() 直接写出
直接写出![]() 的面积与四边形
的面积与四边形![]() 的面积的比值 .
的面积的比值 .
【答案】(1)证明见解析;(2)①![]() ;②
;②![]()
【解析】
(1) 连接![]() ,根据圆周角定理得到
,根据圆周角定理得到![]() ,因此得到
,因此得到![]() ,再根据
,再根据![]() 以及直线平行的性质即可证明;
以及直线平行的性质即可证明;
(2) ①由![]() 得
得![]() ,假设
,假设![]() ,根据
,根据![]() 即可计算r的值,进而得到直径AB的值;
即可计算r的值,进而得到直径AB的值;
②作![]() 于
于![]() 先根据垂径定理算出BD=9,再设
先根据垂径定理算出BD=9,再设![]() 中
中![]() 边的高长度为
边的高长度为![]() ,设
,设![]() 中
中![]() 边的高长度为
边的高长度为![]() ,根据
,根据![]() 即可算出答案;
即可算出答案;
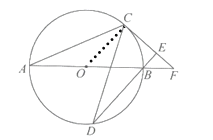
解:(1)连接![]() ,
,
∵![]() (圆周角定理),
(圆周角定理),
∴![]()
∴![]() (内错角相等,两直线平行),
(内错角相等,两直线平行),
又由![]()
∴![]()
∴![]() (两直线平行,同旁内角互补),
(两直线平行,同旁内角互补),
故![]() 与
与![]() 相切.
相切.
(2)①如图,
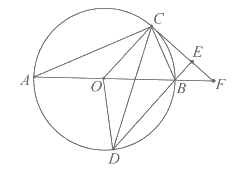
由(1)知![]() (两直线平行,同位角相等),
(两直线平行,同位角相等),
又![]() (同弧圆周角相等),
(同弧圆周角相等),
∴![]()
∴![]() ,
,
设![]() ,
,
则![]() ,
,
于是![]()
解得![]() ,
,
则![]() .
.
②如图1,作![]() 于
于![]()
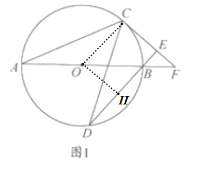
则![]()
由垂径定理得![]() .
.
如图2,设![]() 中
中![]() 边的高长度为
边的高长度为![]() ,设
,设![]() 中
中![]() 边的高长度为
边的高长度为![]() ,
,
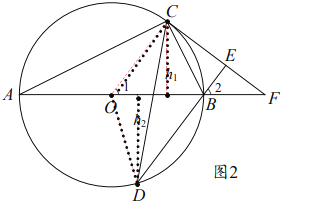
则![]()
记![]() ,
,
则![]() ,
,![]() ,
,
得面积比为![]() ;
;

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
【题目】某市一研究机构为了了解![]() 岁年龄段市民对创建文明城市的关注程度,随机选取了
岁年龄段市民对创建文明城市的关注程度,随机选取了![]() 名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别 | 年龄段 | 频数(人数) |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
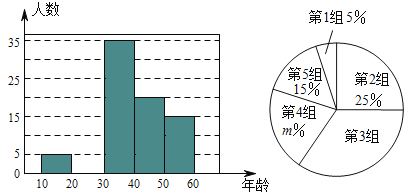
(1)请直接写出![]() ,第
,第![]() 组人数在扇形统计图中所对应的圆心角是 度;
组人数在扇形统计图中所对应的圆心角是 度;
(2)请补全上面的频数分布直方图:
(3)假设该市现有![]() 岁的市民
岁的市民![]() 万人,问
万人,问![]() 岁年龄段的关注创建文明城市的人数约有多少?
岁年龄段的关注创建文明城市的人数约有多少?