题目内容
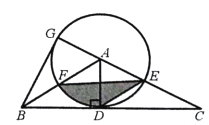
【题目】有理数a,b,c,ab<0,ac>0,且|c|>|b|>|a|,数轴上a,b,c对应的点分别为A,B,C.
(1)若a=1,请你在数轴上标出点A,B,C的大致位置;
(2)若|a|=﹣a,则a 0,b 0,c 0;(填“>”、“<“或“=”)
(3)小明判断|a﹣b|﹣|b+c|+|c﹣a|的值一定是正数,小明的判断是否正确?请说明理由.
【答案】(1)在数轴上标出点A,B,C的大致位置如图见解析;(2)<,>,<;(3)小明的判断正确.理由见解析.
【解析】
(1)a=1时,易得b<0,c>0,再利用|c|>|b|>|a|得到c>1,-c<b<-1,然后在数轴上大致标出数b、c即可;
(2)根据绝对值的意义得到a<0,则由ab<0,ac>0易得b>0,c<0;
(3)讨论:当a>0时,则b<0,c>0,再由|c|>|b|>|a|得到a-b>0,b+c>0,c-a>0,然后根据绝对值的意义去绝对值合并得到原式=-2b,从而得到原式的值为正数;当a<0时,同样方法得到原式的值为正数,于是判断|a-b|-|b+c|+|c-a|的值一定是正数.
(1)a=1时,b<0,c>0,
而|c|>|b|>|a|,
所以c>1,﹣c<b<﹣1,
如图,
![]()
(2)∵|a|=﹣a,
∴a<0,
∴b>0,c<0,
故答案为<,>,<;
(3)小明的判断正确.理由如下:
当a>0时,则b<0,c>0,
而|c|>|b|>|a|,
则|a﹣b|﹣|b+c|+|c﹣a|=a﹣b﹣(b+c)+c﹣a=﹣2b>0;
当a<0时,则b>0,c<0,
而|c|>|b|>|a|,
则|a﹣b|﹣|b+c|+|c﹣a|=﹣(a﹣b)+(b+c)+a﹣c=2b>0;
综上所述,|a﹣b|﹣|b+c|+|c﹣a|的值一定是正数.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案【题目】某初中学校欲向高一级学校推荐一名学生,根据规定的推荐程序:首先由本年级200名学生民主投票,每人只能推荐一人(不设弃权票),选出了票数最多的甲、乙、丙三人.投票结果统计如图一:

其次,对三名候选人进行了笔试和面试两项测试.各项成绩如下表所示:
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 92 | 90 | 95 |
面试 | 85 | 95 | 80 |
图二是某同学根据上表绘制的一个不完全的条形图.
请你根据以上信息解答下列问题:
(1)补全图一和图二;
(2)请计算每名候选人的得票数;
(3)若每名候选人得一票记1分,投票、笔试、面试三项得分按照2:5:3的比确定,计算三名候选人的平均成绩,成绩高的将被录取,应该录取谁?