Question

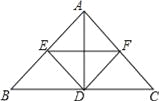
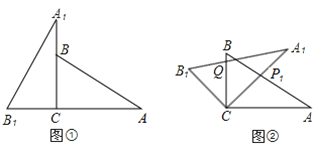
【题目】将两块全等的三角板如图①摆放，其中∠A1CB1=∠ACB=90°，∠A1=∠A=30°．

（1）将图①中的△A1B1C顺时针旋转45°得图②，点P1是A1C与AB的交点，点Q是A1B1与BC的交点，求证：CP1=CQ；

（2）在图②中，若AP1=2，则CQ等于多少？

Answer 1

【答案】（1）证明见解析；（2）CQ=

【解析】（1）利用△A1CB1≌△ACB得到CA1=CA，再根据旋转的性质得∠B1CB=∠A1CA=45°，则∠BCA1=45°，于是根据“ASA”判断△CQA1≌△CP1A，所以CP1=CQ；

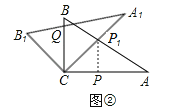
（2）过点P1作P1P⊥AC于点P，如图②，先在Rt△AP1P中根据含30度的直角三角形三边的关系得到P1P=AP1=×2=1，然后在Rt△CP1P中利用等腰直角三角形的性质得CP=P1P=1，CP1=PP1=，由（1）得CQ=CP1=．

（1）∵△A1CB1≌△ACB，∴CA1=CA．

∵图①中的△A1B1C顺时针旋转45°得图②，∴∠B1CB=∠A1CA=45°，∴∠BCA1=45°．

在△CQA1和△CP1A中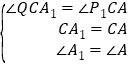，∵，∴△CQA1≌△CP1A，∴CP1=CQ；

（2）过点P1作P1P⊥AC于点P，如图②．在Rt△AP1P中，∵∠A=30°，∴P1P=AP1=×2=1．在Rt△CP1P中，∵∠P1CP=45°，∴CP=P1P=1，∴CP1=PP1=，∴CQ=CP1=．