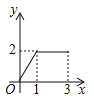题目内容
【题目】点P，Q分别从A，B两点同时出发，在数轴上运动，它们的速度分别是2个单位长度/s、4个单位长度/s，它们运动的时间为t s.
(1)如果点P，Q在点A，B之间相向运动，当它们相遇时，点P对应的数是________；
(2)如果点P，Q都向左运动，当点Q追上点P时，求点P对应的数；
(3)如果点P，Q在点A，B之间相向运动，当PQ＝8时，求点P对应的数．
【答案】（1）
；（2）-40；（3）
或0.
【解析】
（1）由题意列出关于t的一元一次方程，求出t的值，进而可求出点P所对应的数；
（2）由题意列出关于t的一元一次方程，求出t的值，进而可求出点P所对应的数；
（3）分两种情况，列出关于t的一元一次方程，分别求出t的值，进而可求出点P所对应的数.
（1）由数轴上的点A，点B的位置，可知：AB=
，
由题意得：2t+4t=28，解得：t=
，
此时，AP=2×=
，
点P对应的数为：-12+=，
故答案为：；
（2）由题意得：2t+28=4t，解得：t=14，
此时，点P对应的数为：-12-14×2=-40；
（3）①若相遇前PQ＝8时，
则2t+8+4t=28，解得：t=
，
此时，点P对应的数为-12+×2=，
②若相遇后PQ＝8时，
则2t-8+4t=28，解得：t=6，
此时，点P对应的数为-12+6×2=0，
综上所述：点P对应的数为或0.
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
【题目】观察理解，并解决问题.
问题情境：如图所示，用一些相同的小正方形，拼在一起，排成如下的一些大正方形：
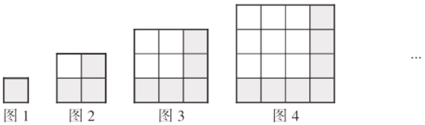
问题解决：（1）完成下表：
图序号 | 1 | 2 | 3 | 4 | … |
|
每一行小正方形的个数 | 1 | 2 | 3 | ______ | … | ______ |
阴影小正方形的个数 | 1 | 3 | 5 | ______ | … | ______ |
（2）根据图形规律推测：
______（用含
的代数式表示）
（3）像（1），（2）这样，根据某类事物的部分对象具有的某种性质，推出这类事物的所有对象具有的这种性质的推理，叫做归纳推理.对于科学的发现，归纳推理是十分有用的，通过观察、实验，对有限个对象的性质作归纳整理，提出对某类事物带有规律性的猜测，是科学研究的基本方法.请观察下列等式的规律：第一个等式：
；第二个等式：
；第三个等式：
；…猜想并直接写出第个等式.（用含的代数式表示）
