题目内容
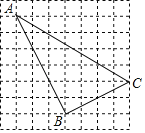
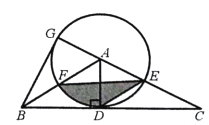
【题目】如图,在△ABC中,过点A作AD⊥BC,垂足为点D,以AD为半径的⊙A分别与边AC、AB交于点E和点F,DE∥AB,延长CA交⊙A于点G,连接BG.
(1)求证:BG是⊙A的切线;
(2)若∠ACB=30°,AD=3,求图中阴影部分的面积.
【答案】(1)证明见解析(2)![]()
【解析】分析:(1) 根据DE∥AB得出∠BAD=∠ADE,∠GAB=∠AED,再依据AD=AE得出∠BAD=∠GAB,从而证明△GAB≌△DAB,即可得出∠ADB=∠AGB =90°,从而说明BG是⊙A的切线;
(2)证四边形AFDE为菱形,从而得到阴影部分的面积等于扇形AFD的面积.
详解:
(1)∵DE∥AB
∴∠BAD=∠ADE,∠GAB=∠AED
∵AD=AE

∴∠AED=∠ADE
∴∠BAD=∠GAB
在△GAB和△DAB中
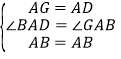
∴△GAB≌△DAB
∴∠AGB =∠ADB
∵AD⊥BC
∴∠ADB=90°
∴∠AGB =90°
∴BG是⊙A的切线.
(2)连接FD
∵∠ACB=30°,∠ADC=90°
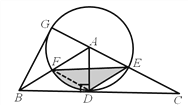
∴∠CAD=60°
∵AD=AE
∴△ADE为等边三角形
∴DE=AE=AF
又∵DE∥AB
∴四边形AFDE为菱形
∴AE∥FD
∴S△AFD= S△EFD
∴S阴影= S扇形AFD
∵∠FAD=60°,AD=3
∴S阴影= S扇形AFD=![]()
点睛: 本题考查了等腰三角形的性质,平行线的性质和判定,切线的判定,三角形的面积,扇形的面积计算等知识点,主要考查学生综合运用定理进行推理的能力,综合性比较强,有一定的难度.

【题目】在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
分 组 | 频数 | 频率 |
第一组(0≤x<15) | 3 | 0.15 |
第二组(15≤x<30) | 6 | a |
第三组(30≤x<45) | 7 | 0.35 |
第四组(45≤x<60) | b | 0.20 |
(1)频数分布表中a=_____,b=_____,并将统计图补充完整;
(2)如果该校七年级共有女生180人,估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人?
(3)已知第一组中只有一个甲班学生,第四组中只有一个乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?