题目内容
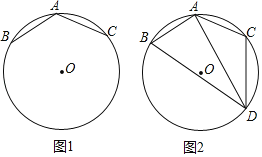
【题目】如图1,已知A、B、C是⊙O上的三点,AB=AC,∠BAC=120°.
(1)求证:⊙O的半径R=AB;
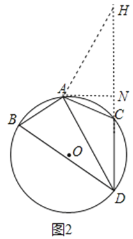
(2)如图2,若点D是∠BAC所对弧上的一动点,连接DA,DB,DC.
①探究DA,DB,DC三者之间的数量关系,并说明理由;
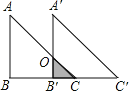
②若AB=3,点C'与C关于AD对称,连接C'D,点E是C'D的中点,当点D从点B运动到点C时,求点E的运动路径长.
【答案】(1)见解析;(2)①CD+BD=![]() AD,见解析,②2
AD,见解析,②2![]() π
π
【解析】
(1)连接OA,OB,OC,由“SSS”可证△OAB≌△OAC,可得∠BAO=∠CAO=60°,可证△ABO是等边三角形,可得结论;
(2)将△ABD绕点A逆时针旋转120°得到△ACH,过点A作AN⊥CH于N,由旋转的性质可得BD=CH,AD=AH,∠DAH=120°,∠ABD=∠ACH,可证点D,点C,点H三点共线,由直角三角形的性质可求解;
(3)先确定点E的运动轨迹,利用弧长公式可求解.
证明:(1)如图1,连接OA,OB,OC,
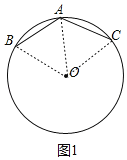
∵AB=AC,OB=OC,OA=OA,
∴△OAB≌△OAC(SSS),
∴∠BAO=∠CAO,
又∵∠BAC=120°,
∴∠OAB=60°=∠OAC,
∴△ABO是等边三角形,
∴⊙O的半径R=AB;
(2)CD+BD=![]() AD,
AD,
理由如下:如图2,将△ABD绕点A逆时针旋转120°得到△ACH,过点A作AN⊥CH于N,
∴BD=CH,AD=AH,∠DAH=120°,∠ABD=∠ACH,
∵四边形ABDC是圆内接四边形,
∴∠ABD+∠ACD=180°,
∴∠ACD+∠ACH=180°,
∴点D,点C,点H三点共线,
∵AD=AH,∠DAH=120°,AN⊥CH,
∴∠AHD=∠ADH=30°,HN=DN=![]() DH,
DH,
∴AD=2AN,DN=![]() AN,
AN,
∴HD=![]() AN=
AN=![]() AD,
AD,
∴CD+CH=CD+BD=![]() AD;
AD;
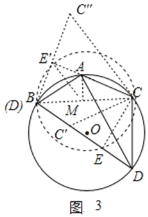
(3)如图3,连接BC,过点A作AM⊥BC于M,连接CC',CE,
∵AB=AC,∠BAC=120°,AM⊥BC,AB=3,
∴∠ABC=∠ACB=30°,
∴AM=![]() ,BM=
,BM=![]() AM=
AM=![]() ,
,
∵∠ADB=∠ACB=30°,∠ADC=∠ABC=30°,
∴∠ADB=∠ADC,
∴点C关于AD对称点C'在BD上,
∴CD=C'D,
又∵∠CDC'=60°,
∴△CDC'是等边三角形,
∵点E是C'D的中点,
∴CE⊥BD,
∴点E在以BC为直径的圆上,
当点B与点D重合时,
∵E'M=BM=CM,
∴∠MCE'=∠ME'C=30°,
∴∠BME'=60°,
当点D与点C重合时,点E也与点C重合,
∴点E的运动路径长=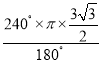 =2
=2![]() π.
π.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案