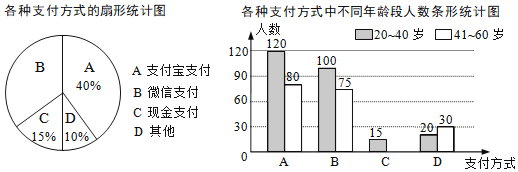
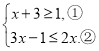题目内容
【题目】如图,在平面直角坐标系中,四边形![]() 是矩形,点
是矩形,点![]() ,点
,点![]() ,点
,点![]() ;D为
;D为![]() 边上的动点.
边上的动点.
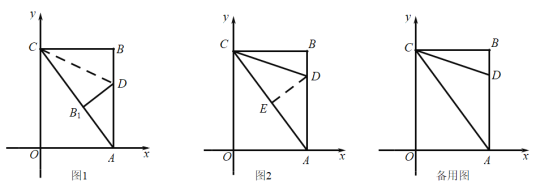
(Ⅰ)如图1,将![]() 对折,使得点B的对应点
对折,使得点B的对应点![]() 落在对角线
落在对角线![]() 上,折痕为
上,折痕为![]() ,求此刻点D的坐标;
,求此刻点D的坐标;
(Ⅱ)如图2,将![]() 对折,使得点A的与点C重合,折痕交
对折,使得点A的与点C重合,折痕交![]() 于点D,交
于点D,交![]() 于点E,求直线
于点E,求直线![]() 的解析式;
的解析式;
(Ⅲ)在坐标平面内,是否存在点P(除点B外),使得![]() 与
与![]() 全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)存在,点P的坐标为
;(Ⅲ)存在,点P的坐标为![]() ,
,![]() 或
或![]()
【解析】
(Ⅰ)根据题意由翻折可知:![]() ,并设
,并设![]() ,由勾股定理得:
,由勾股定理得:![]() ,即
,即![]() 进行求解即可;
进行求解即可;
(Ⅱ)由题意设D点坐标为![]() ,由翻折可知:
,由翻折可知:![]() ,
,![]() ,进而利用勾股定理与待定系数法即可求出直线
,进而利用勾股定理与待定系数法即可求出直线![]() 的解析式;
的解析式;
(Ⅲ)根据题意将点P在不同象限进行分类,根据全等三角形的判定方法找出所有全等三角形,找出符合题意的点P的坐标.
解:(Ⅰ)∵在矩形![]() 中,点
中,点![]() ,点
,点![]() ;
;
∴![]() ,
,![]() ;
;
在![]() 中,
中,![]()
由翻折可知:![]()
∴![]() ,
,![]() ,
,![]()
设![]() ,则
,则![]()
在![]() 中,
中,![]() ,
,![]()
由勾股定理得:![]() ,即
,即![]()
解得:![]() .
.
∵点D在![]() 边上,
边上,
∴D点坐标为![]() .
.
(Ⅱ)设D点坐标为![]()
则![]() ,
,![]()
由翻折可知:![]() ,
,![]() ,
,
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,即
,即![]()
解得:![]()
∴![]()
设直线![]() 的解析式为
的解析式为![]() ,
,
则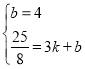 ,解得
,解得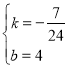 ,
,
∴直线![]() 的解析式为
的解析式为![]() .
.
(Ⅲ)存在点P(除点B外),使得![]() 与
与![]() 全等,理由如下:
全等,理由如下:
①当点P与点O重合时,△APC≌△CBA,此时P(0,0),
②当点P在第一象限时,如图作![]() 交AB 于H,
交AB 于H,
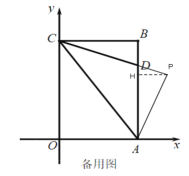
在Rt△ADP中,![]() ,
,
由![]() 得
得![]() ,有P的横轴坐标为:
,有P的横轴坐标为:![]() ,
,
将![]() 代入
代入![]() 的解析式
的解析式![]() ,得到P的纵轴坐标为:
,得到P的纵轴坐标为:![]() ,此时点P的坐标为
,此时点P的坐标为![]() ;
;
③当点P在第一象限时,如图作![]() 交OC 于G,
交OC 于G,
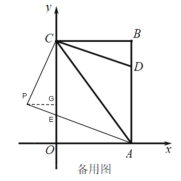
同理可得:![]() ,
,
由勾股定理可得:![]() 解得
解得![]() ,
,
即有![]() ,所以此时点P的坐标为
,所以此时点P的坐标为![]() ;
;
综上符合条件的点P的坐标为![]() ,
,![]() 或
或![]() .
.

 口算题卡北京妇女儿童出版社系列答案
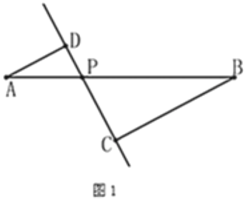
口算题卡北京妇女儿童出版社系列答案【题目】如图1,线段![]() 及一定点
及一定点![]() ,
,![]() 是线段
是线段![]() 上一动点(
上一动点(![]() 、
、![]() 除外),作直线
除外),作直线![]() ,使
,使![]() 于点
于点![]() ,作直线
,作直线![]() ,使
,使![]() 于点
于点![]() .已知
.已知![]() ,
,![]() ,设
,设![]() ,
,![]() ,数学学习小组根据学习函数的经验,对
,数学学习小组根据学习函数的经验,对![]() 与
与![]() 之间的内在关系进行探究.
之间的内在关系进行探究.
(1)写出y与![]() 之间的关系和
之间的关系和![]() 的取值范围;
的取值范围;
活动操作:
(2)①列表,根据(1)的所求函数关系式讲算并补全表格
| 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
|
| 1.8 | 9 | 21 |
②描点:根据表格中数值,继续在图2中描出剩余的三个点![]() ;
;
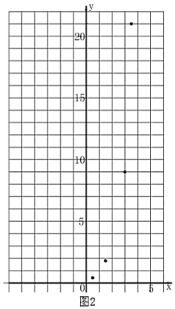
③连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象.
数学思考:
(3)请你结合函数的图象,写出该函数的一条性质或结论.
(4)将该函数图象向上移3个单位,再向左平移4个单位后,直接写出平移后的函数关系式和![]() 的取值范围.
的取值范围.