题目内容
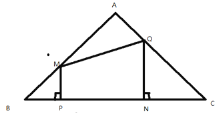
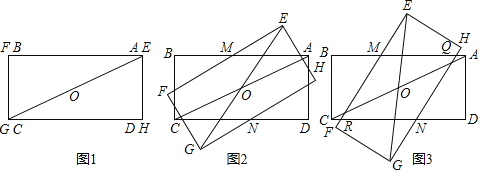
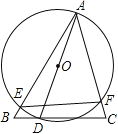
【题目】如图,△ABC中,∠B=60,∠ACB=75,点D是BC边上一动点,以AD为直径作⊙O,分别交AB、AC于E、F,若弦EF的最小值为1,则AB的长为
A. | B. | C.1.5 | D. |
【答案】B
【解析】
首先连接OE,OF,过O点作OH⊥EF,垂足为H,可求得半径OE的长,又由当AD为△ABC的边BC上的高时,AD最大时为直径,OE最大,OH最大,EF最小,可求得AD的长,由三角函数的性质,即可求得AB的长.
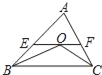
 解:如图,连接OE,OF,过O点作OH⊥EF,垂足为H,
解:如图,连接OE,OF,过O点作OH⊥EF,垂足为H,
∴EH=FH=![]() EF=
EF=![]() ×1=
×1=![]() ,
,
∵在△ADB中,∠B=60°,∠ACB=75°,
∴∠BAC=45°,
∴∠EOF=2∠BAC=90°,
∵OE=OF,
∴∠EOH=![]() ∠EOF=45°,
∠EOF=45°,
∴OE=![]() =
=![]() ,
,
∵当AD为△ABC的边BC上的高时,AD最大时为直径,OE最大,OH最大,EF最小,
∴AD=2OE=![]() ,
,
∴AB=![]() =
=![]()
故选:B.

练习册系列答案
相关题目
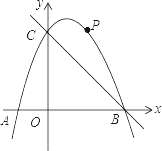
【题目】已知二次函数的解析式是y=x2﹣2x﹣3.
(1)与y轴的交点坐标是 ,顶点坐标是 .
(2)在坐标系中利用描点法画出此抛物线;
x | … | … | |||||
y | … | … |
(3)结合图象回答:当﹣2<x<2时,函数值y的取值范围是 .