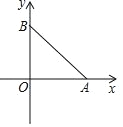ЬтФПФкШн
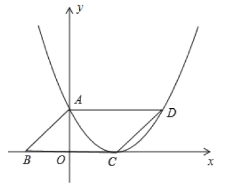
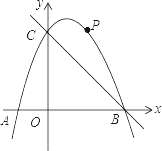
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЖўДЮКЏЪ§yЃНЉx2+bx+cЕФЭМЯѓгыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкCЃЈ0ЃЌ3ЃЉЃЌAЕудкдЕуЕФзѓВрЃЌBЕуЕФзјБъЮЊЃЈ3ЃЌ0ЃЉЃЎЕуPЪЧХзЮяЯпЩЯвЛИіЖЏЕуЃЌЧвдкжБЯпBCЕФЩЯЗНЃЎ
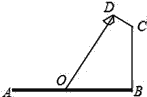
ЃЈ1ЃЉЧѓетИіЖўДЮКЏЪ§ЕФБэДяЪНЃЎ
ЃЈ2ЃЉСЌНгPOЁЂPCЃЌВЂАбЁїPOCбиCOЗелЃЌЕУЕНЫФБпаЮPOPЁфCЃЌФЧУДЪЧЗёДцдкЕуPЃЌЪЙЫФБпаЮPOPЁфCЮЊСтаЮЃПШєДцдкЃЌЧыЧѓГіДЫЪБЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
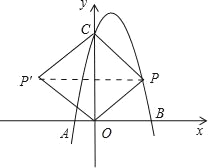
ЃЈ3ЃЉЕБЕуPдЫЖЏЕНЪВУДЮЛжУЪБЃЌЫФБпаЮ ABPCЕФУцЛ§зюДѓЃЌВЂЧѓГіДЫЪБЕуPЕФзјБъКЭЫФБпаЮABPCЕФзюДѓУцЛ§ЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃНЉx2+2x+3ЃЛЃЈ2ЃЉPЕуЕФзјБъЮЊ![]() ЃЛЃЈ3ЃЉPЕуЕФзјБъЮЊ
ЃЛЃЈ3ЃЉPЕуЕФзјБъЮЊ![]() ЃЌЫФБпаЮABPCУцЛ§ЕФзюДѓжЕЮЊ
ЃЌЫФБпаЮABPCУцЛ§ЕФзюДѓжЕЮЊ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнД§ЖЈЯЕЪ§ЗЈЃЌПЩЕУКЏЪ§НтЮіЪНЃЛЃЈ2ЃЉИљОнСтаЮЕФЖдНЧЯпЛЅЯрЦНЗжЃЌПЩЕУPЕуЕФзнзјБъЃЌИљОнКЏЪ§жЕгыздБфСПЕФЖдгІЙиЯЕЃЌПЩЕУД№АИЃЛЃЈ3ЃЉИљОнУцЛ§ЕФКЭВюЃЌПЩЕУЖўДЮКЏЪ§ЃЌИљОнЖўДЮКЏЪ§ЕФаджЪЃЌПЩЕУmЕФжЕЃЌИљОнздБфСПгыКЏЪ§жЕЕФЖдгІЙиЯЕЃЌПЩЕУPЕузјБъЃЎ
НтЃКЃЈ1ЃЉНЋBЁЂCСНЕуЕФзјБъДњШыЕУ![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЎ
ЃЎ
ЫљвдЖўДЮКЏЪ§ЕФБэДяЪНЮЊyЃНЉx2+2x+3ЃЛ
ЃЈ2ЃЉШчЭМЃЌ
 ЃЌ
ЃЌ
ДцдкЕуPЃЌЪЙЫФБпаЮPOPЁфCЮЊСтаЮЃЎ
ЩшPЕузјБъЮЊЃЈxЃЌЉx2+2x+3ЃЉЃЌ
PPЁфНЛCOгкE
ШєЫФБпаЮPOPCЪЧСтаЮЃЌдђгаPCЃНPOЃЎ
СЌНгPPдђPEЁЭCOгкEЃЎ
ЁрOEЃНCEЃН![]() ЃЌ
ЃЌ
ЁрyЃН![]() ЃЎ
ЃЎ
ЁрЉx2+2x+3=![]() ЃЌ
ЃЌ
НтЕУx1ЃН![]() ЃЌx2ЃН
ЃЌx2ЃН![]() ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉ
ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉ
ЁрPЕуЕФзјБъЮЊ![]() ЃЎ
ЃЎ
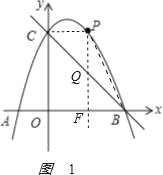
ЃЈ3ЃЉШчЭМ1ЃЌ
 ЃЌ
ЃЌ
Й§ЕуPзїyжсЕФЦНааЯпгыBCНЛгкЕуQЃЌгыOBНЛгкЕуFЃЌЩшPЃЈxЃЌЉx2+2x+3ЃЉ
взЕУЃЌжБЯпBCЕФНтЮіЪНЮЊyЃНЉx+3ЃЎ
дђQЕуЕФзјБъЮЊЃЈxЃЌЉx+3ЃЉЃЎ
PQЃНЉx2+3xЃЎ
SЫФБпаЮABPCЃНSЁїABC+SЁїBPQ+SЁїCPQЃН![]() ABOC+
ABOC+![]() QPBF+
QPBF+![]() QPOF
QPOF
ЃН![]() ЁС4ЁС3+
ЁС4ЁС3+![]() ЃЈЉx2+3xЃЉЁС3
ЃЈЉx2+3xЃЉЁС3
ЃНЉ![]() ЃЈxЉ
ЃЈxЉ![]() ЃЉ2+
ЃЉ2+![]() ЃЌ
ЃЌ
ЕБx=![]() ЪБЃЌЫФБпаЮABPCЕФУцЛ§зюДѓ
ЪБЃЌЫФБпаЮABPCЕФУцЛ§зюДѓ
ДЫЪБPЕуЕФзјБъЮЊ![]() ЃЌЫФБпаЮABPCУцЛ§ЕФзюДѓжЕЮЊ
ЃЌЫФБпаЮABPCУцЛ§ЕФзюДѓжЕЮЊ![]() ЃЎ
ЃЎ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ