Question

【题目】如图，在矩形OABC中，OA＝8，OC＝4，OA、OC分别在x轴与y轴上，D为OA上一点，且CD＝AD．

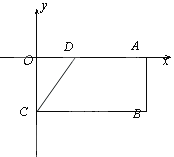
（1）求点D的坐标；

（2）若经过B、C、D三点的抛物线与x轴的另一个交点为E，请直接写出点E的坐标；

（3）在（2）中的抛物线上位于x轴上方的部分，是否存在一点P，使△PBC的面积等于梯形DCBE的面积？若存在，求出点P的坐标，若不存在，请说明理由．

Answer 1

【答案】（1）D（3，0）；（2）E（5，0）；（3）不存在

【解析】

（1）设OD＝x，则AD＝CD＝8－x ，在Rt△OCD中，根据勾股定理即可列方程求解；

（2）由题意知，抛物线的对称轴为直线x＝4，根据抛物线的对称性即可求得结果；

（3）若存在这样的P，则由S梯形＝20得S△PBC＝·BC·h＝20可求得h＝5，根据待定系数法求得抛物线函数关系式，从而得到顶点坐标，即可得到顶点到BC的距离为4＋＝＜5，即可作出判断.

（1）设OD＝x，则AD＝CD＝8－x

Rt△OCD中，(8－x)2＝x2＋42，得x＝3

∴OD＝3

∴D（3，0）

（2）由题意知，抛物线的对称轴为直线x＝4

∵D（3，0）， ∴另一交点E（5，0）

（3）若存在这样的P，则由S梯形＝20得S△PBC＝·BC·h＝20．

∴h＝5

∵B（8，－4）， C（0，－4）， D（3，0）

∴该抛物线函数关系式为：y＝－x2＋x－4．

顶点坐标为（4，）

∴顶点到BC的距离为4＋＝＜5

∴不存在这样的点P， 使得△PBC的面积等于梯形DCBE的面积．