题目内容
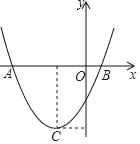
【题目】已知二次函数的解析式是y=x2﹣2x﹣3.
(1)与y轴的交点坐标是 ,顶点坐标是 .
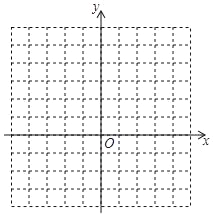
(2)在坐标系中利用描点法画出此抛物线;
x | … | … | |||||
y | … | … |
(3)结合图象回答:当﹣2<x<2时,函数值y的取值范围是 .
【答案】(1)与y轴交点的坐标为(0,﹣3),顶点坐标为(1,﹣4);(2)图象如图所示见解析;(3)-2<x<2时,﹣4<y<5.
【解析】
(1)令x=0,根据y=x2﹣2x﹣3,可以求得抛物线与y轴的交点,把解析式化成顶点式即可求得顶点坐标;
(2)根据第一问中的三个坐标和二次函数图象具有对称性,在表格中填入合适的数据,然后再描点作图即可;
(3)根据第二问中的函数图象结合对称轴可以直接写出答案.
(1)令x=0,则y=﹣3.
所以抛物线y=x2﹣2x﹣3与y轴交点的坐标为(0,﹣3),
y=x2﹣2x﹣3=(x﹣1)x2﹣4,
所以它的顶点坐标为(1,﹣4);
故答案为(0,﹣3),(1,﹣4);
(2)列表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | … |
图象如图所示:
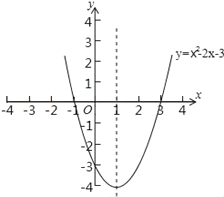 ;
;
(3)当﹣2<x<1时,﹣4<y<5;
当1<x<2时,﹣4<y<﹣3.所以-2<x<2时,-4<y<5

练习册系列答案
相关题目