Question

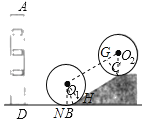
【题目】如图，水平地面上有一幢高为AD的楼，楼前有坡角为30°、长为6米的斜坡．已知从A点观测B、C的俯角分别为60°和30°

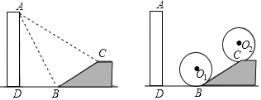
（1）求楼高；

（2）现在要将一个半径为2米的⊙O从坡底与斜坡相切时的⊙O1位置牵引滚动到斜坡上至圆刚好与斜坡上水平面相切时的⊙O2位置，求滚动过程中圆心O移动的总长度．（参考数据：tan15°＝2﹣）

Answer 1

【答案】（1）楼高为9米；（2）滚动过程中圆心O移动的总长度为（3+2）米．

【解析】

（1）由题意可得，可得，又因斜坡的坡角为，可得，在中，可求出AB的长，从而在中可求出楼高AD；

（2）如图（见解析），设⊙切BC于H，连接，作于N，作于G，连接，先在四边形得出，从而可以得出，，在和中，分别利用三角函数值求出和的长，再求出的长，即为所求.

（1）由题意得：

又因斜坡的坡角为，斜坡长为6米

在中，，则

在中，，则

故楼高为9米；

（2）如图，设⊙切BC于H，连接，作于N，作于G，连接

则

斜坡的坡角为

⊙切BC于H

在中，

由切线的性质得：

在中，

故滚动过程中圆心O移动的总长度为米.