题目内容
【题目】综合与实践:矩形的旋转
问题情境:
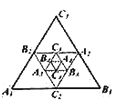
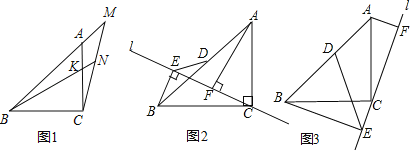
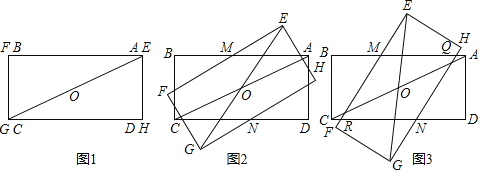
在综合与实践课上,老师让同学们以“矩形的旋转”为主题开展数学活动.具体要求:如图1,将长与宽都相等的两个矩形纸片ABCD和EFGH叠放在一起,这时对角线AC和EG互相重合.固定矩形ABCD,将矩形EFGH绕AC的中点O逆时针方向旋转,直到点E与点B重合时停止,在此过程中开展探究活动.
操作发现:
(1)雄鹰小组初步发现:在旋转过程中,当边AB与EF交于点M,边CD与GH交于点N,如图2、图3所示,则线段AM与CN始终存在的数量关系是 .
(2)雄鹰小组继续探究发现:在旋转开始后,当两个矩形纸片重叠部分为四边形QMRN时,如图3所示,四边形QMRN为菱形,请你证明这个结论.
(3)雄鹰小组还发现在问题(2)中的四边形QMRN中∠MQN与旋转角∠AOE存在着特定的数量关系,请你写出这一关系,并说明理由.
实践探究:
(4)在图3中,随着矩形纸片EFGH的旋转,四边形QMRN的面积会发生变化.若矩形纸片的长为![]() ,宽为
,宽为![]() ,请你帮助雄鹰小组探究当旋转角∠AOE为多少度时,四边形QMRN的面积最大?最大面积是多少?(直接写出答案)
,请你帮助雄鹰小组探究当旋转角∠AOE为多少度时,四边形QMRN的面积最大?最大面积是多少?(直接写出答案)
【答案】(1)结论:AM=CN,理由见解析;
(2)证明见解析;
(3)结论:∠MQN=∠AOE,理由见解析;
(4)∠AOE=45°或135°时,四边形QMRN面积最大为![]() .
.
【解析】
(1)先证明△AOK≌△AOJ(ASA),推出OK=OJ,AK=CJ,∠AOK=∠AJO,再证明△EKM≌△GJN(ASA)即可的解;(2)过点Q作QK⊥EF,QL⊥CD,垂足分别为点K,L、先证明四边形QMRN是平行四边形,再证明QM=QN即可的解;(3)由三角形的外角的性质以及平行线的性质即可解决问题;(4)如图3-2中,连接BD,在DC上取一点J,使得DJ=AD=![]() ,则AJ=2,通过解直角三角形求出∠BOC的度数,再结合图象即可得解.
,则AJ=2,通过解直角三角形求出∠BOC的度数,再结合图象即可得解.
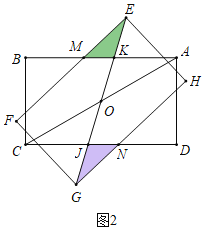
(1)结论:AM=CN.
理由:如图2中,设AB交EG于K,CD交EG于J.
∵四边形ABCD是矩形,四边形EFGH是矩形,
∴AB∥CD,EF∥EG,OA=OC=OE=OG,
∴∠MEK=∠JGN,∠OAK=∠OAJ,
∵∠AOK=∠AOJ,∴△AOK≌△AOJ(ASA),
∴OK=OJ,AK=CJ,∠AOK=∠AJO,∴EK=JG,
∵∠EKM=∠AKO,∠GJN=∠CJO,∴∠EKM=∠GJN,
∴△EKM≌△GJN(ASA),∴KM=JN,∴AM=AN.
(2)证明:过点Q作QK⊥EF,QL⊥CD,垂足分别为点K,L.
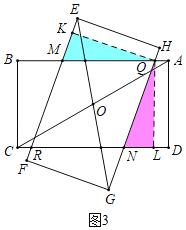
由题可知:矩形ABCD≌矩形EFGH,
∴AD=EH,AB∥CD,EF∥HG,
∴四边形QMRN为平行四边形,
∵QK⊥EF,QL⊥CD,∴QK=EH,QL=AD,∠QKM=∠QLN=90°,∴QK=QL,
又∵AB∥CD,EF∥HG,∴∠KMQ=∠MQN,∠MQN=∠LNQ,
∴∠KMQ=∠LNQ,∴△QKM≌△QLN(AAS),
∴MQ=NQ∴四边形QMRN为菱形.
(3)结论:∠MQN=∠AOE.理由:如图3﹣1中,
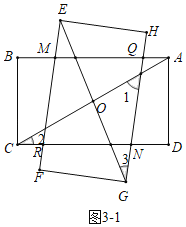
∵∠QND=∠1+∠2,∠AOE=∠1+∠3,
又由题意可知旋转前∠2与∠3重合,∴∠2=∠3,∴∠QND═∠AOE,
∵AB∥CD,∴∠MQN=∠QND,∴∠MQN=∠AOE.
(4)如图3﹣2中,连接BD,在DC上取一点J,使得DJ=AD=![]() ,则AJ=2,
,则AJ=2,
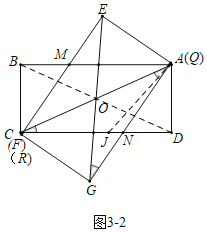
∵CD=2+![]() ,∴CJ=AJ=2,∴∠JCA=∠JAC,
,∴CJ=AJ=2,∴∠JCA=∠JAC,
∵∠AJD=45°=∠JCA+∠JAC,∴∠ACJ=22.5°,
∵OC=OD,∴∠OCD=∠ODC=22.5°,∴∠BOC=45°,
观察图象可知,当点F与点C重合或点G与点D重合时,四边形QMRN的面积最大,最大值=![]() ,
,
∴∠AOE=45°或135°时,四边形QMRN面积最大为![]() .
.