题目内容
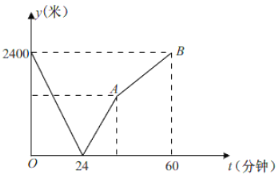
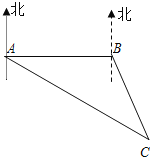
【题目】如图，
为任意三角形，以边
为边分别向外作等边三角形
和等边三角形
，连接
、
并且相交于点
．求
的度数．
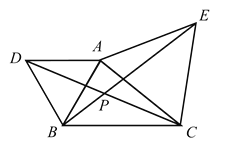
【答案】120°
【解析】
根据等边三角形的性质得出AD=AB，AE=AC，∠ACE=∠AEC=60°，∠DAB=∠EAC=60°，求出∠DAC=∠BAE，根据SAS推出△DAC≌△BAE，然后利用全等三角形的性质和三角形的外角性质求解即可．
解：∵以AB、AC为边分别向外做等边△ABD和等边△ACE，
∴AD=AB，AE=AC，∠ACE=∠AEC=60°，∠DAB=∠EAC=60°，
∴∠DAB+∠BAC=∠EAC+∠BAC，
∴∠DAC=∠BAE，
在△DAC和△BAE中，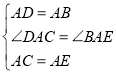
，
∴△DAC≌△BAE（SAS），
∴∠ACD=∠AEB
∵∠BPC=∠BEC+∠DCE
∴∠BPC=∠BEC+∠ACD+∠ACE
=∠BEC+∠AEB+∠ACE
=∠AEC+∠ACE
=120°．
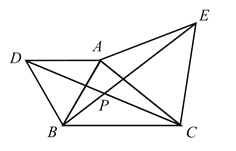
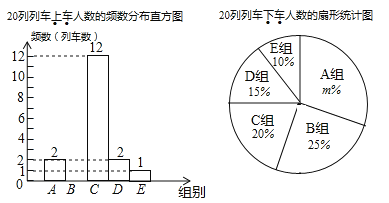
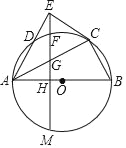
【题目】根据重庆轨道集团提供的日客运量统计，2019年2月21日重庆轨道交通首次日客运量突破300万乘次，其中近期开通的重庆轨道交通环线日客运量为21.5万乘次．据了解，某工作日上午7点至9点轨道环线四公里站有20列列车进出站，每列车进出站时，将上车和下车的人数记录下来，各得到20个数据，并将数据进行整理，绘制成了如下两幅不完整统计图．(数据分组为：
组：
，
组：
，
组：
，
组：
，
组：
)
I．上车人数在组的是：190，190，191，192，193，193，195，196，198，198，198，198；
II．上车人数的平均数、中位数如下表：
平均数 | 中位数 | |
上车人数(人) | 194 | a |
根据以上信息，回答下列问题：
(1)请补全频数分布直方图；
(2)表中
________，扇形统计图中
_________，扇形统计图中组所在的圆心角度数为________度；
(3)请利用平均数，估算一周内5个工作日的上午7点至9点重庆轨道环线四公里站的上车总人数．
