题目内容
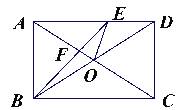
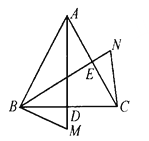
【题目】如图,AD、BE分别是等边△ABC中BC、AC上的高.M、N分别在AD、BE的延长线上,∠CBM=∠ACN.求证:AM=BN.
【答案】见解析
【解析】
根据等边三角形的性质可得∠ABC=∠ACB=60°,AB=BC,然后求出∠ABM=∠BCN,再根据等边三角形三线合一的性质求出∠BAM=∠CBN=30°,然后利用“角边角”证明△ABM和△BCN全等,再根据全等三角形对应边相等证明即可.
:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,AB=BC,
∵∠CBM=∠ACN,
∴∠ABC+∠CBM=∠ACB+∠ACN,
即∠ABM=∠BCN,
∵AD、BE分别是边BC、AC上的高,
∴∠BAM=∠CBN=30°,
在△ABM和△BCN中,
∠ABM=∠BCN AB=BC ∠BAM=∠CBN,
∴△ABM≌△BCN(ASA),
∴AM=BN.

练习册系列答案
相关题目