题目内容
【题目】如图,直线![]() 与
与![]() 轴交于点A,与
轴交于点A,与![]() 轴交于点B,抛物线
轴交于点B,抛物线![]() 经过原点和点C(4,0),顶点D在直线AB上。
经过原点和点C(4,0),顶点D在直线AB上。
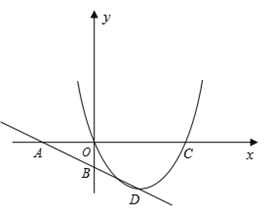
(1)求这个抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使得以P、C、D为顶点的三角形与△ACD相似。若存在,请求出点P的坐标;若不存在,请说明理由;
(3)点Q是![]() 轴上方的抛物线上的一个动点,若
轴上方的抛物线上的一个动点,若![]() ,⊙M经过点O,C,Q,求过C点且与⊙M相切的直线解析式
,⊙M经过点O,C,Q,求过C点且与⊙M相切的直线解析式
【答案】(1)![]() ;(2)点
;(2)点![]() ;(3)
;(3)![]() .
.
【解析】试题分析: ![]() 先求出点
先求出点![]() 的坐标,把点
的坐标,把点![]() 的坐标代入抛物线即可求出抛物线的解析式.
的坐标代入抛物线即可求出抛物线的解析式.
![]() 分两种情况进行讨论.
分两种情况进行讨论.
![]() 在
在![]() 中,用余弦得到
中,用余弦得到![]() 设
设![]() 根据勾股定理求出
根据勾股定理求出![]() 的值,求出点
的值,求出点![]() 的坐标,根据待定系数法求出直线的解析式.
的坐标,根据待定系数法求出直线的解析式.
试题解析:
(1)由题知:D点的横坐标为2,
∴![]() ,
,
![]() 把
把![]() 代入抛物线:
代入抛物线: ![]() 解之得:
解之得: 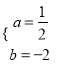
∴抛物线的解析式为: ![]()
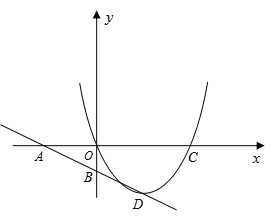
(2)存在点![]()
设对称轴与![]() 轴交于点
轴交于点![]() ,
, ![]()
易知: ![]()
![]()
情况1: ![]() 点在
点在![]() 点上方,则
点上方,则![]()
若![]() 则
则![]()
∴![]() 解得:
解得: ![]() ,
,
∴![]() .
.
若![]() 则
则![]()
![]() 解得:
解得: ![]()
∴ ![]() .
.
情况2:若P在D点的下方,则![]() 没有一个角会为
没有一个角会为![]()
∴![]() 与
与![]() 不可能相似
不可能相似
综上可知:存在点![]()
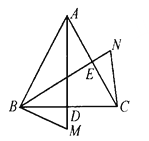
(3)、设![]() 与
与![]() 轴交于点
轴交于点![]() ,连NC交抛物线对称轴于一点,即为圆心M点,
,连NC交抛物线对称轴于一点,即为圆心M点,

![]()
在![]() 中,
中, ![]()
![]() 设
设![]()
则: 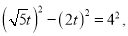 解得:
解得: ![]()
![]() ∴点
∴点![]() 坐标为(0,8),
坐标为(0,8),
![]()
设过点![]() 且与
且与![]() 相切的直线为
相切的直线为![]()
则![]() ,把
,把![]() 点代入有:
点代入有: ![]() ,解得:
,解得: ![]()
∴过点![]() 且与
且与![]() 相切的直线为
相切的直线为 ![]() .
.

练习册系列答案
相关题目