题目内容
【题目】综合与实践
问题情境
如图,同学们用矩形纸片ABCD开展数学探究活动,其中AD=8,CD=6。
操作计算
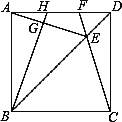
(1)如图(1),分别沿BE,DF剪去RtΔABE和RtΔCDF两张纸片,如果剩余的纸片BEDF菱形,求AE的长;

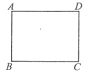
图(1) 图(2) 图(3)
操作探究
把矩形纸片ABCD沿对角线AC剪开,得到ΔABC和![]() 两张纸片
两张纸片
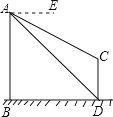
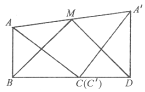
(2)将两张纸片如图(2)摆放,点C和![]() 重合,点B,C,D在同一条直线上,连接
重合,点B,C,D在同一条直线上,连接![]() ,记
,记![]() 的中点为M,连接BM,MD,发现ΔBMD是等腰三角形,请证明:
的中点为M,连接BM,MD,发现ΔBMD是等腰三角形,请证明:
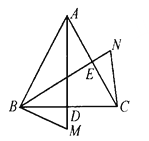
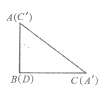
(3)如图(3),将两张纸片叠合在一起,然后将![]() 纸片绕点B顺时针旋转a(00<a<900),连接
纸片绕点B顺时针旋转a(00<a<900),连接![]() 和
和![]() ,探究并直接写出线段
,探究并直接写出线段![]() 与
与![]() 的关系。
的关系。
【答案】(1)AE的长为![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】试题分析:(1)由矩形的性质得出AB=CD=6,∠A=90°,由菱形的性质得出BE=DE=AD-AE=8-AE,在Rt△ABE中,由勾股定理得出方程,解方程即可;
(2)连接MC,证出△ACA’是等腰直角三角形,得出∠CA’A=45°,由直角三角形斜边上的中线性质和等腰三角形的性质得出A’M=CM=AM,∠MCA=45°,CM⊥AA’,证出∠BCM=∠DA’M,由SAS证明△BCM≌△DA’M,得出BM=DM,∠BMC=∠DMA’,由角的雇佣关系证出∠BMD=90°,即可得出结论;
(3)延长AC’、A’C交于点M,由旋转的性质得:BC’=BA,BA’=BC,∠A’BC=∠ABC,∠BA’C=∠BC’A,证出∠BAC=∠BC’A=∠BCA’=∠BA’C,由四边形内角和定理得出∠A’BC’+∠M=180°,证出∠M=90°,得出AC’⊥A’C,证明△ABC’∽△C’BA’,得出对应边成比例![]() ,即可求得AC’=
,即可求得AC’=![]() A’C.
A’C.
试题解析:
(1)解:∵四边形ABCD是矩形,AD=8,CD=6,
∴AB=CD=6,∠A=90°,
∵四边形BEDF是菱形,
∴BE=DE=AD-AE=8-AE,
在Rt△ABE中,由勾股定理得:AB2+AE2=BE2,
即62+AE2=(8-AE)2,
解得:AE=![]() ;
;
(2)证明:连接MC,如图2所示:
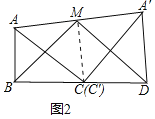
根据题意得:△ABC≌△CDA’,∠CDA’=90°,
∴AC=A’C,∠BCA=∠CA’D,∠CA’D+∠A’CD=90°,
∴∠BCA+∠A’CD=90°,
∵点B,C,D在同一条直线上,
∴∠ACA’=90°,
∴△ACA’是等腰直角三角形,
∴∠CA’A=45°,
∵M是AA’的中点,
∴A’M=CM=AM,∠MCA=45°,CM⊥AA’,
∵∠BCA=∠CA’D,
∴∠BCA+∠MCA=∠CA’D+∠CA’A,
∴∠BCM=∠DA’M,
在△BCM和△DA’M中,
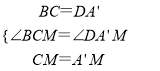
∴△BCM≌△DA’M(SAS),
∴BM=DM,∠BMC=∠DMA’,
∵∠CMD+∠DMA’=90°,
∴∠CMD+∠BMC=90°,
∴∠BMD=90°,
∴△BMD是等腰直角三角形;
(3)解:AC’⊥A’C,AC’=![]() A’C,理由如下:
A’C,理由如下:
延长AC’、A’C交于点M,如图3所示:
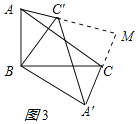
由旋转的性质得:BC’=BA,BA’=BC,∠A’BC=∠ABC,∠BA’C=∠BC’A,
∴∠BAC=∠BC’A,∠BCA’=∠BA’C,
∴∠BAC=∠BC’A=∠BCA’=∠BA’C,
∵∠BC’A+∠BC’M=180°,
∴∠BA’C+∠BC’M=180°,
∴∠A’BC’+∠M=180°,
∵∠A’BC’=∠ABC=90°,
∴∠M=90°,
∴AC’⊥A’C,
∵∠BAC=∠BC’A=∠BCA’=∠BA’C,
∴△ABC’∽△C’BA’,
∴![]() ,
,
∴AC’=![]() A’C.
A’C.

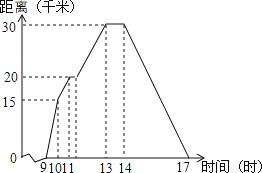
【题目】为了解某校八年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:![]() )绘制成不完整的频数分布表和频数分布直方图.
)绘制成不完整的频数分布表和频数分布直方图.
学生立定路远测试成绩的频数分布表
分组 | 频数 |
|
|
| 12 |
|
|
| 10 |
请根据图表中所提供的信息,完成下列问题:
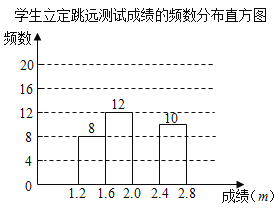
(1)求表中![]() ,
,![]() 的值;
的值;
(2)请把频数分布直方图补充完整;
(3)该校八年级共有800名学生,估计该年级学生立定跳远成绩在![]() 范围内的学生有多少人?
范围内的学生有多少人?