题目内容
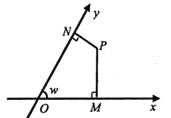
【题目】定义:在同一平面内画两条相交、有公共原点的数轴x轴和y轴,交角a≠90°,这样就在平面上建立了一个斜角坐标系,其中w叫做坐标角,对于坐标平面内任意一点P,过P作y轴和x轴的平行线,与x轴、y轴相交的点的坐标分别是a和b,则称点P的斜角坐标为(a,b).如图,w=60°,点P的斜角坐标是(1,2),过点P作x轴和y轴的垂线,垂足分别为M、N,则四边形OMPN的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.3
D.3
【答案】B
【解析】
添加辅助线,将四边形OMPN转化为直角三角形和平行四边形,因此过点P作PA∥y轴,交x轴于点A,过点P作PB∥x轴交y轴于点B,易证四边形OAPB是平行四边形,利用平行四边形的性质,可知OB=PA,OA=PB,由点P的斜角坐标就可求出PB、PA的长,再利用解直角三角形分别求出PN,NB,PM,AM的长,然后根据S四边形OMPN=S△PAM+S△PBN+S平行四边形OAPB , 利用三角形的面积公式和平行四边形的面积公式,就可求出结果.
解:过点P作PA∥y轴,交x轴于点A,过点P作PB∥x轴交y轴于点B,
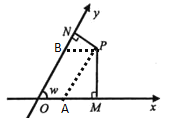
∴四边形OAPB是平行四边形,∠NBP=w=∠PAM=60°,
∴OB=PA,OA=PB
∵点P的斜角坐标为(1,2),
∴OA=1,OB=2,
∴PB=1,PA=2,
∵PM⊥x轴,PN⊥y轴,
∴∠PMA=∠PNB=90°,
在Rt△PAM中,∠PAM=60°,则∠APM=30°,
∴PA=2AM=2,即AM=1
PM=PAsin60°
∴PM=![]()
∴S△PAM=![]()
在Rt△PBN中,∠PBN=60°,则∠BPN=30°,
∴PB=2BN=1,即BN=![]()
PN=PBsin60°
∴PN=![]()
∴S△PBN=![]() ,
,
∵S四边形OMPN=S△PAM+S△PBN+S平行四边形OAPB
![]()
故答案为:B