题目内容
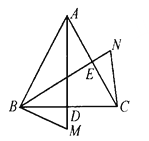
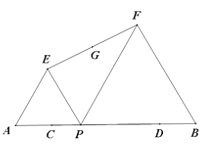
【题目】如图,已知AB=10,点C,D在线段AB上且AC=DB=2;P是线段CD上的动点,分别以AP,PB为边在线段AB的同侧作等边△AEP和等边△PFB,连接EF,设EF的中点为G;当点P从点C运动到点D时,则点G移动路径的长是( ).
A.6B.5C.4D.3.
【答案】D
【解析】
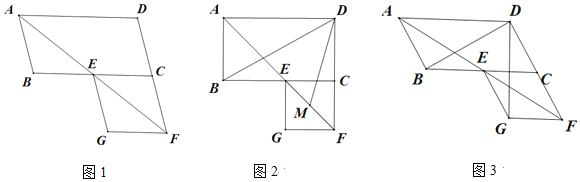
分别延长AE、BF交于点H,易证四边形EPFH为平行四边形,得出G为PH中点,则G的运行轨迹为三角形HCD的中位线MN.再求出CD的长,运用中位线的性质求出MN的长度即可.
如图,分别延长AE、BF交于点H.

∵∠A=∠FPB=60°,
∴AH∥PF,
∵∠B=∠EPA=60°,
∴BH∥PE,
∴四边形EPFH为平行四边形,
∴EF与HP互相平分.
∵G为EF的中点,
∴G也正好为PH中点,
即在P的运动过程中,G始终为PH的中点,
所以G的运行轨迹为三角形HCD的中位线MN.
∵CD=10-2-2=6,
∴MN=3,即G的移动路径长为3.
故选:D.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
【题目】用A4纸复印文件,在甲复印店不管一次复印多少页,每页收费0.1元.在乙复印店复印同样的文件,一次复印页数不超过20时,每页收费0.12元;一次复印页数超过20时,超过部分每页收费0.09元.设在同一家复印店一次复印文件的页数为![]() (
(![]() 为非负整数).
为非负整数).
(1)根据题意,填写下表:
一次复印页数(页) | 5 | 10 | 20 | 30 | … |
甲复印店收费(元) |
| 2 | … | ||
乙复印店收费(元) |
|
| … |
(2)设在甲复印店复印收费![]() 元,在乙复印店复印收费
元,在乙复印店复印收费![]() 元,分别写出
元,分别写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)当![]() 时,顾客在哪家复印店复印花费少?请说明理由.
时,顾客在哪家复印店复印花费少?请说明理由.