题目内容
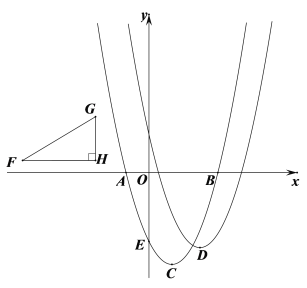
【题目】如图二次函数的图象与![]() 轴交于点
轴交于点![]() 和
和![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 、
、![]() 是二次函数图象上的一对对称点,一次函数的图象经过
是二次函数图象上的一对对称点,一次函数的图象经过![]() 、
、![]()

(1)求二次函数的解析式;
(2)写出使一次函数值大于二次函数值的![]() 的取值范围;
的取值范围;
(3)若直线![]() 与
与![]() 轴的交点为
轴的交点为![]() 点,连结
点,连结![]() 、
、![]() ,求
,求![]() 的面积;
的面积;
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)4.
;(3)4.
【解析】
(1)直接将已知点代入函数解析式求出即可;
(2)利用函数图象结合交点坐标得出使一次函数值大于二次函数值的x的取值范围;
(3)分别得出EO,AB的长,进而得出面积.
(1)∵二次函数与![]() 轴的交点为
轴的交点为![]() 和
和![]()
∴设二次函数的解析式为:![]()
∵![]() 在抛物线上,
在抛物线上,
∴3=a(0+3)(0-1),
解得a=-1,
所以解析式为:![]() ;
;
(2)![]() =x22x+3,
=x22x+3,
∴二次函数的对称轴为直线![]() ;
;
∵点![]() 、
、![]() 是二次函数图象上的一对对称点;
是二次函数图象上的一对对称点;![]()
∴![]() ;
;
∴使一次函数大于二次函数的![]() 的取值范围为
的取值范围为![]() 或
或![]() ;
;
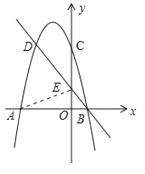
(3)设直线BD:y=mx+n,
代入B(1,0),D(2,3)得![]() ,
,
解得:![]() ,
,
故直线BD的解析式为:y=x+1,
把x=0代入![]() 得,y=3,
得,y=3,
所以E(0,1),
∴OE=1,
又∵AB=4,
∴S△ADE=![]() ×4×3
×4×3![]() ×4×1=4.
×4×1=4.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目