题目内容
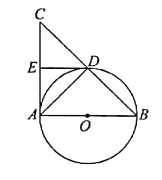
【题目】如图，点
是
中
边的中点，
于
，以
为直径的
经过，连接
，有下列结论：①
;②
;③
;④
是的切线.其中正确的结论是（ ）
A.①②B.①②③C.②③D.①②③④
【答案】D
【解析】
由直径所对的圆周角是直角，即可判断出选项①正确；由O为AB的中点，得出AO为AB 的一半，故AO为AC的一半,选项③正确；由OD为三角形ABC的中位线，根据中位线定理得到OD与AC平行，由AC与DE垂直得出OD与DE垂直，
，选项④正确；由切线性质可判断②正确.
解：∵AB是圆的直径，∴
，∴
，选项①正确；
连接OD,如图，
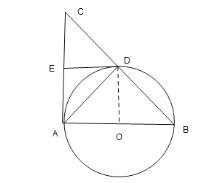
∵D为BC的中点，O为AB的中点，∴DO为
的中位线，
∴
，
又∵
，∴
,∴,∴DE为圆O的切线，选项④正确；
又OB=OD,
∴
，
∵AB为圆的直径，∴
∵
∴
∴
，选项②正确；
∴AD垂直平方BC，
∵AC=AB，2OA=AB
∴
，选项③正确
故答案为：D.
练习册系列答案
相关题目
