题目内容
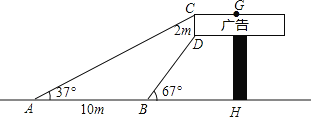
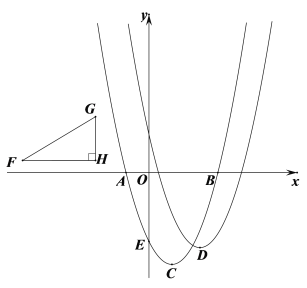
【题目】如图,Rt△FHG中,![]() H=90°,FH∥x轴,
H=90°,FH∥x轴,![]() ,则称Rt△FHG为准黄金直角三角形(G在F的右上方).已知二次函数
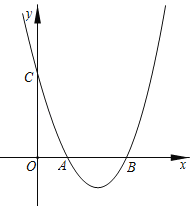
,则称Rt△FHG为准黄金直角三角形(G在F的右上方).已知二次函数![]() 的图像与x轴交于A、B两点,与y轴交于点E(0,
的图像与x轴交于A、B两点,与y轴交于点E(0,![]() ),顶点为C(1,
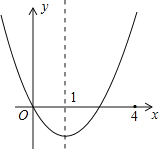
),顶点为C(1,![]() ),点D为二次函数
),点D为二次函数![]() 图像的顶点.
图像的顶点.
(1)求二次函数y1的函数关系式;
(2)若准黄金直角三角形的顶点F与点A重合、G落在二次函数y1的图像上,求点G的坐标及△FHG的面积;
(3)设一次函数y=mx+m与函数y1、y2的图像对称轴右侧曲线分别交于点P、Q. 且P、Q两点分别与准黄金直角三角形的顶点F、G重合,求m的值并判断以C、D、Q、P为顶点的四边形形状,请说明理由.
【答案】(1)y=(x-1)2-4;(2)点G坐标为(3.6,2.76),S△FHG=6.348;(3)m=0.6,四边形CDPQ为平行四边形,理由见解析.
【解析】
(1)利用顶点式求解即可,(2)将G点代入函数解析式求出坐标,利用坐标的特点即可求出面积,(3)作出图象,延长QH,交x轴于点R,由平行线的性质得证明△AQR∽△PHQ,设Q[n,0.6(n+1)],代入y=mx+m中,即可证明四边形CDPQ为平行四边形.
(1)设二次函数的解析式是y=a(x-h)2+k,(a≠0),由题可知该抛物线与y轴交于点E(0,![]() ),顶点为C(1,
),顶点为C(1,![]() ),
),
∴y=a(x-1)2-4,代入E(0,![]() ),解得a=1,
),解得a=1,
![]() (
(![]() )
)
(2)设G[a,0.6(a+1)],代入函数关系式,
得,![]() ,
,
解得a1=3.6,a2=-1(舍去),
所以点G坐标为(3.6,2.76).
S△FHG=6.348
(3)y=mx+m=m(x+1),
当x=-1时,y=0,
所以直线y=mx+m
延长QH,交x轴于点R,
由平行线的性质得,QR⊥x轴.
因为FH∥x轴,
所以∠QPH=∠QAR,
因为∠PHQ=∠ARQ=90°,
所以△AQR∽△PQH,
所以![]() =0.6,
=0.6,
设Q[n,0.6(n+1)],代入y=mx+m中,
mn+m=0.6(n+1),m(n+1)=0.6(n+1),
因为n+1≠0,
所以m=0.6..
因为y2=(x-1-m)2+0.6m-4,
所以点D由点C向右平移m个单位,再向上平移0.6m个单位所得,
过D作y轴的平行线,交x轴与K,再作CT⊥KD,交KD延长线与T,
所以![]() =0.6,
=0.6,
所以tan∠KSD=tan∠QAR,
所以∠KSD=∠QAR,
所以AQ∥CS,即CD∥PQ.
因为AQ∥CS,由抛物线平移的性质可得,CT=PH,DT=QH,
所以PQ=CD,
所以四边形CDPQ为平行四边形.


 高中必刷题系列答案
高中必刷题系列答案