题目内容
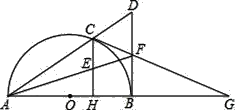
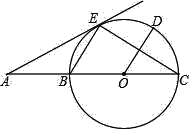
【题目】如图,BC是⊙O的直径,D、E是⊙O上的两点,且弧CD=DE,连接EB、DO.
(1)求证:EB∥DO;
(2)连接EC,在∠CEB的外部作∠BEA=∠C,直线EA交CB的延长线于A,求证:直线EA是⊙O的切线;
(3)若EA=2,AB=1,求⊙O的半径长.
【答案】(1)见解析;(2)见解析;(3)⊙O半径长为![]() .
.
【解析】
(1)由垂径定理得:OD⊥EC;由圆周角定理,得:BE⊥EC;由此可证得EB∥DO;
(2)连接OE,证得∠OEA=90°即可;
(3)根据AE2=ABAC,即可求得AC长,进而求得⊙O的半径长.
(1)∵弧CD=DE,
∴OD⊥EC,
∵BC是⊙O的直径,
∴∠BEC=90°,
∴BE⊥EC,
∴EB∥DO;
(2)连接OE,
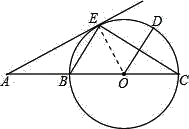
∵OC=OE,
∴∠C=∠OEC,
∵∠BEA=∠C,
∴∠BEA=∠OEC,
∵∠CEO+∠BEO=90°,
∴∠BEA+∠BEO=90°,即∠OEA=90°,
∴直线EA是⊙O的切线;
(3)∵AE是切线,AC是割线,
∴由切割线定理知:AE2=ABAC,
∴AC=AE2÷AB=4,
∴BC=AC﹣AB=3,
∴⊙O半径长为![]() .
.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目