题目内容
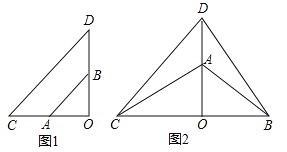
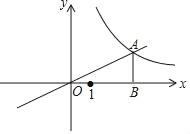
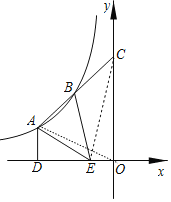
【题目】如图,点A、B是反比例函数y=![]() (k≠0)图象上的两点,延长线段AB交y 轴于点C,且点B为线段AC中点,过点A作AD⊥x轴子点D,点E 为线段OD的三等分点,且OE<DE.连接AE、BE,若S△ABE=7,则k的值为( )
(k≠0)图象上的两点,延长线段AB交y 轴于点C,且点B为线段AC中点,过点A作AD⊥x轴子点D,点E 为线段OD的三等分点,且OE<DE.连接AE、BE,若S△ABE=7,则k的值为( )

A. ﹣12 B. ﹣10 C. ﹣9 D. ﹣6
【答案】A
【解析】
设A(m,![]() ),C(0,n),则D(m,0),E(
),C(0,n),则D(m,0),E(![]() m,0),由AB=BC,推出B(
m,0),由AB=BC,推出B(![]() ,
,![]() ),根据点B在y=
),根据点B在y=![]() 上,推出
上,推出![]()
![]() =k,可得mn=3k,连接EC,OA.因为AB=BC,推出S△AEC=2S△AEB=14,根据S△AEC=S△AEO+S△ACO-S△ECO,构建方程即可解决问题.
=k,可得mn=3k,连接EC,OA.因为AB=BC,推出S△AEC=2S△AEB=14,根据S△AEC=S△AEO+S△ACO-S△ECO,构建方程即可解决问题.
解:设A(m,![]() ),C(0,n),则D(m,0),E(
),C(0,n),则D(m,0),E(![]() m,0),
m,0),
∵AB=BC,
∴B(![]() ,
,![]() ),
),
∵点B在y=![]() 上,
上,
∴![]()
![]() =k,
=k,
∴k+mn=4k,
∴mn=3k,
连接EC,OA.
∵AB=BC,
∴S△AEC=2S△AEB=14,
∵S△AEC=S△AEO+S△ACO-S△ECO,
∴14=![]() (-
(-![]() m)
m)![]() +
+![]() n(-m)-
n(-m)-![]() (-
(-![]() m)n,
m)n,
∴14=-![]() k-
k-![]() +
+![]() ,
,
∴k=-12.
故选:A.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
【题目】甲、乙两人参加射击比赛,两人成绩如图所示.
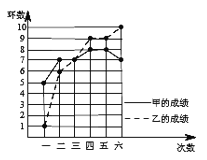
(1)填表:
平均数 | 方差 | 中位数 | 众数 | |
甲 | 7 | 1 | 7 | |
乙 | 9 |
(2)只看平均数和方差,成绩更好的是 .(填“甲”或“乙”)
(3)仅就折线图上两人射击命中环数的走势看,更有潜力的是 .(填“甲”或“乙”)