Question

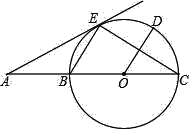
【题目】如图，⊙M交x轴于B、C两点，交y轴于A，点M的纵坐标为2．B（﹣3，O），C（，O）．

（1）求⊙M的半径；

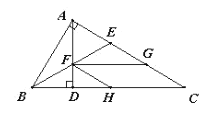
（2）若CE⊥AB于H，交y轴于F，求证：EH=FH．

（3）在（2）的条件下求AF的长．

Answer 1

【答案】（1）4；（2）见解析;（3）4．

【解析】

（1）过M作MT⊥BC于T连BM，由垂径定理可求出BT的长，再由勾股定理即可求出BM的长；

（2）连接AE，由圆周角定理可得出∠AEC=∠ABC，再由AAS定理得出△AEH≌△AFH，进而可得出结论；

（3）先由（1）中△BMT的边长确定出∠BMT的度数，再由直角三角形的性质可求出CG的长，由平行四边形的判定定理判断出四边形AFCG为平行四边形，进而可求出答案．

（1）如图（一），过M作MT⊥BC于T连BM，

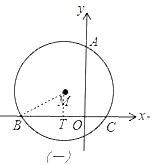
∵BC是⊙O的一条弦，MT是垂直于BC的直径，

∴BT=TC=BC=2，

∴BM==4；

（2）如图（二），连接AE，则∠AEC=∠ABC，

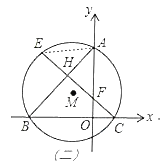
∵CE⊥AB，

∴∠HBC+∠BCH=90°

在△COF中，

∵∠OFC+∠OCF=90°，

∴∠HBC=∠OFC=∠AFH，

在△AEH和△AFH中，

∵，

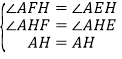∴△AEH≌△AFH（AAS），

∴EH=FH；

（3）由（1）易知，∠BMT=∠BAC=60°，

作直径BG，连CG，则∠BGC=∠BAC=60°，

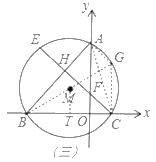
∵⊙O的半径为4，

∴CG=4，

连AG，

∵∠BCG=90°，

∴CG⊥x轴，

∴CG∥AF，

∵∠BAG=90°，

∴AG⊥AB，

∵CE⊥AB，

∴AG∥CE，

∴四边形AFCG为口，

∴AF=CG=4．