题目内容
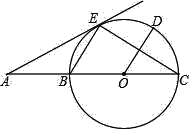
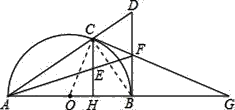
【题目】如图,已知:C是以AB为直径的半圆O上一点,CH⊥AB于点H,直线AC与过B点的切线相交于点D,E为CH中点,连接AE并延长交BD于点F,直线CF交直线AB于点G.
(1)求证:点F是BD中点;
(2)求证:CG是⊙O的切线;
(3)若FB=FE=2,求⊙O的半径.
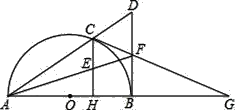
【答案】(1)见解析;(2)见解析;(3)⊙O半径为2![]() .
.
【解析】
(1)由已知中CH⊥AB于点H,DB为圆的切线,我们易得到△AEH∽AFB,△ACE∽△ADF,进而根据三角形相似,对应边成比例,根据E为CH中点,得到点F是BD中点;
(2)连接CB、OC,根据圆周定理的推论,我们易得在直角三角形BCD中CF=BF,进而求出∠OCF=90°,由切线的判定定理,得到CG是⊙O的切线;
(3)由由FC=FB=FE,易得FA=FG,且AB=BG,由切割线定理及勾股定理,我们可以求出AB的长,即圆的直径,进而得到圆的半径.
(1)∵CH⊥AB,DB⊥AB,
∴△AEH∽△AFB,△ACE∽△ADF,
∴![]() ,
,
∵HE=EC,
∴BF=FD,即点F是BD中点;
(2)连接CB、OC,
∵AB是直径,
∴∠ACB=90°,
∵F是BD中点,
∴∠BCF=∠CBF=90°﹣∠CBA=∠CAB=∠ACO,
∴∠OCF=90°,
又∵OC为圆O半径,
∴CG是⊙O的切线,
(3)∵FC=FB=FE,
∴∠FCE=∠FEC,
∵∠FEC=∠AEH,
∴∠FCE=∠AEH,
∵∠G+∠FCE=90°,∠FAB+∠AEH=90°,
∴∠G=∠FAB,
∴FA=FG,
∵FB⊥AG,
∴AB=BG,
∵(2+FG)2=BG×AG=2BG2①
BG2=FG2﹣BF2②
由①、②得:FG2﹣4FG﹣12=0,
∴FG1=6,FG2=﹣2(舍去),
∴AB=BG=![]() ,
,
∴⊙O半径为2![]() .
.

练习册系列答案
相关题目