题目内容
【题目】阅读材料:“直角三角形如果有一个角等于![]() ,那么这个角所对的边等于斜边的一半”,即“在
,那么这个角所对的边等于斜边的一半”,即“在![]() 中,
中,![]() ,则
,则![]() ”.利用以上知识解决下列问题:如图,已知
”.利用以上知识解决下列问题:如图,已知![]() 是
是![]() 的平分线上一点.
的平分线上一点.
(1)若![]() 与射线
与射线![]() 分别相交于点
分别相交于点![]() ,且
,且![]() .
.
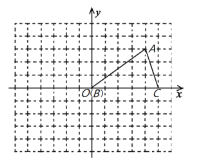
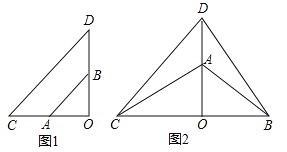
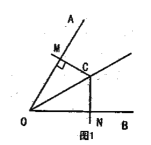
①如图1,当![]() 时,求证:
时,求证: ![]() ;
;
②当![]() 时,求
时,求![]() 的值.
的值.
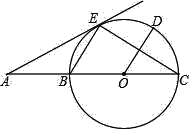
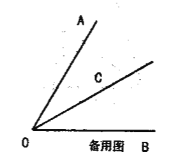
(2)若![]() 与射线
与射线![]() 的反向延长线、射线
的反向延长线、射线![]() 分别相交于点
分别相交于点![]() ,且
,且![]() ,请你直接写出线段
,请你直接写出线段![]() 三者之间的等量关系.
三者之间的等量关系.
【答案】(1)①证明见解析;②![]() ;(2)OM-ON=
;(2)OM-ON=![]()
【解析】
(1)①根据题意证明CNO=90°及∠COM=∠CON=30°,可利用题目中信息得到OM=ON,再利用勾股定理即可解答;
②证明△COM≌CON,得到∠CMO=∠CNO=90°,再利用①中结论即可;
(2)根据题意作出辅助线,再证明△MCE≌△NCF(ASA),得到NF=ME,由30°直角三角形的性质得到OE=OF=![]() ,进而得到OM-ON=
,进而得到OM-ON=![]() 即可.
即可.
(1)①证明:∵CM⊥OA,
∴∠CMO=90°,
∵![]() ,∠MCN=120°,
,∠MCN=120°,
∴∠CNO=360°-∠CMO-∠AOB-∠MCN=90°,
∵C是∠AOB平分线上的一点,
∴CM=CN,∠COM=∠CON=30°,
∵OC=2,
∴CM=CN=1,
由勾股定理可得:OM=ON=![]() ,
,
∴![]()
②当![]() 时,
时,
∵OC是∠AOB的平分线,
∴∠COM=∠CON=30°,
在△COM与CON中

∴△COM≌CON(SAS)
∴∠CMO=∠CNO
∵∠AOB=60°,∠MCN=120°,
∴∠CMO+∠CNO=360°-60°-120°=180°
∴∠CMO=∠CNO=90°,
又①可知![]()
(2)如图所示,作CE⊥OA于点E,作CF⊥OB于点F,
∵∠AOB=60°,
∴∠ECF=120°,
又∵∠MCN=120°,
∴∠MCE+∠ECN=∠NCF+∠ECN
∴∠MCE=∠NCF
∵OC是∠AOB的平分线,
∴∠COM=∠CON=30°,CE=CF
∴在△MCE与△NCF中,
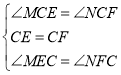
∴△MCE≌△NCF(ASA)
∴NF=ME
又∵△OCE≌△OCF,∠COM=∠CON=30°,
∴CE=CF=![]()
∴OE=OF=![]()
∴OM-OE=ON+OF,
∴OM-ON=OE+OF=![]() ,
,
故答案为:OM-ON=![]()