题目内容
【题目】定义:到一个三角形三个顶点的距离相等的点叫做该三角形的外心.
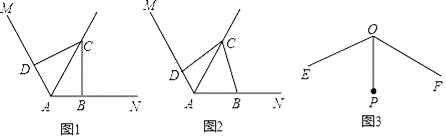
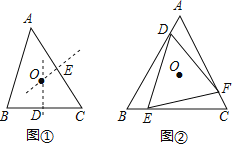
(1)如图①,小海同学在作△ABC的外心时,只作出两边BC,AC的垂直平分线得到交点O,就认定点O是△ABC的外心,你觉得有道理吗?为什么?
(2)如图②,在等边三角形ABC的三边上,分别取点D,E,F,使AD=BE=CF,连接DE,EF,DF,得到△DEF.若点O为△ABC的外心,求证:点O也是△DEF的外心.
【答案】(1)定点O是△ABC的外心有道理,理由见解析;(2)见解析
【解析】
(1)连接![]() 、
、![]() 、
、![]() ,如图①,根据线段垂直平分线的性质得到
,如图①,根据线段垂直平分线的性质得到![]() ,
,![]() ,则
,则![]() ,从而根据三角形的外心的定义判断点
,从而根据三角形的外心的定义判断点![]() 是
是![]() 的外心;
的外心;
(2)连接![]() 、
、![]() 、
、![]() 、
、![]() ,如图②,利用等边三角形的性质得到
,如图②,利用等边三角形的性质得到![]() ,
,![]() ,再计算出
,再计算出![]() ,接着证明
,接着证明![]() 得到
得到![]() ,同理可得
,同理可得![]() ,所以
,所以![]() ,然后根据三角形外心的定义得到点
,然后根据三角形外心的定义得到点![]() 是
是![]() 的外心.
的外心.
(1)解:定点![]() 是
是![]() 的外心有道理.
的外心有道理.
理由如下:
连接![]() 、
、![]() 、
、![]() ,如图①,
,如图①,

![]() ,
,![]() 的垂直平分线得到交点
的垂直平分线得到交点![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 点
点![]() 是
是![]() 的外心;
的外心;
(2)证明:连接![]() 、
、![]() 、
、![]() 、
、![]() ,如图②,
,如图②,
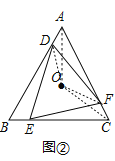
![]() 点
点![]() 为等边
为等边![]() 的外心,
的外心,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中
中
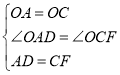 ,
,
![]() ,
,
![]() ,
,
同理可得![]() ,
,
![]() ,
,
![]() 点
点![]() 是
是![]() 的外心.
的外心.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目