题目内容
【题目】如图,四边形ABCD是边长为2的正方形,以点A,B,C为圆心作圆,分别交BA,CB,DC的延长线于点E,F,G.
(1)求点D沿三条圆弧运动到点G所经过的路线长;
(2)判断线段GB与DF的长度关系,并说明理由.
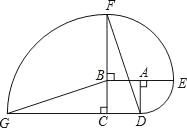
【答案】(1)6π;(2)GB=DF,理由详见解析.
【解析】
(1)根据弧长公式l=![]() 计算即可;
计算即可;
(2)通过证明给出的条件证明△FDC≌△GBC即可得到线段GB与DF的长度关系.
解:(1)∵AD=2,∠DAE=90°,
∴弧DE的长 l1=![]() =π,
=π,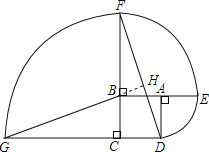
同理弧EF的长 l2=![]() =2π,弧FG的长 l3=
=2π,弧FG的长 l3=![]() =3π,
=3π,
所以,点D运动到点G所经过的路线长l=l1+l2+l3=6π.
(2)GB=DF.
理由如下:延长GB交DF于H.
∵CD=CB,∠DCF=∠BCG,CF=CG,
∴△FDC≌△GBC.
∴GB=DF.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
【题目】甲、乙两人参加射击比赛,两人成绩如图所示.
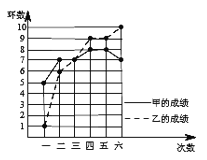
(1)填表:
平均数 | 方差 | 中位数 | 众数 | |
甲 | 7 | 1 | 7 | |
乙 | 9 |
(2)只看平均数和方差,成绩更好的是 .(填“甲”或“乙”)
(3)仅就折线图上两人射击命中环数的走势看,更有潜力的是 .(填“甲”或“乙”)