题目内容
【题目】如图,二次函数y=![]() x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.
(1)求该二次函数的解析式及点C的坐标;
(2)当点P运动到B点时,点Q停止运动,这时,在x轴上是否存在点E,使得以A,E,Q为顶点的三角形为以AQ为腰的等腰三角形?若存在,请求出E点坐标;若不存在,请说明理由.
(3)在AC段的抛物线上有一点R到直线AC的距离最大,请直接写出点R的坐标.


【答案】(1)C(0,﹣4);(2)E点坐标为(﹣1,0),或(7,0)或(﹣![]() ,0);(3) R(
,0);(3) R(![]() ,﹣5)
,﹣5)
【解析】
(1)将A,B点坐标代入函数解析式中,求得b、c,进而可求解析式及C坐标.
(2)等腰三角形有两种情况,AQ=EQ,AE=AQ.易得E坐标.
(3)求出AC解析式,设R的坐标,表示出点R到直线AC的距离,根据二次函数的最值的求法,可求R点坐标.
(1)∵二次函数y=![]() x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),
∴
解得:
∴解析式:y=![]() x2﹣
x2﹣![]() x﹣4
x﹣4
∴C(0,﹣4)
(2)作QD⊥OA于D如图1
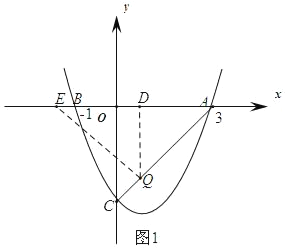
∵A(3,0),B(﹣1,0),C(0,﹣4),O(0,0),
∴AB=4,OA=3,OC=4,
∴AC=![]() =5
=5
∵若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,当点P运动到B点时,点Q停止运动
∴AQ=AB=4
∵QD⊥AB,OC⊥AB
∴QD∥OC
∴![]()
∴![]()
∴QD=![]() ,AD=
,AD=![]()
∵以A,E,Q为顶点的三角形为以AQ为腰的等腰三角形
若当AQ=AE=4时,且A(3,0)
∴E(﹣1,0),或E(7,0)
若当EQ=AQ时,且QD⊥AB
∴DE=AD=![]()
∴E(﹣![]() ,0)
,0)
∴E点坐标为(﹣1,0),或(7,0)或(﹣![]() ,0)
,0)
(3)设AC解析式:y=kx+b
∴![]()
解得:
∴AC解析式:y=![]() x﹣4
x﹣4
设R(x,![]() x2﹣
x2﹣![]() x﹣4),R到直线AC的距离为w
x﹣4),R到直线AC的距离为w
∴w=![]() x﹣4﹣(
x﹣4﹣(![]() x2﹣
x2﹣![]() x﹣4)=﹣
x﹣4)=﹣![]() x2+4x=﹣
x2+4x=﹣![]() (x﹣
(x﹣![]() )2+3
)2+3
∴当x=![]() 时,w最大为3.
时,w最大为3.
∴R(![]() ,﹣5)
,﹣5)