Question

【题目】根据要求回答问题：
（1）【问题发现】
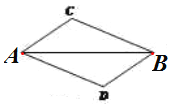
如图1，在Rt△ABC中，AB=AC=2，∠BAC=90°，点D为BC的中点，以CD为一边作正方形CDEF，点E恰好与点A重合，求线段BE与AF的数量关系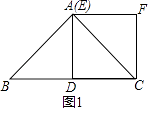

（2）【拓展研究】
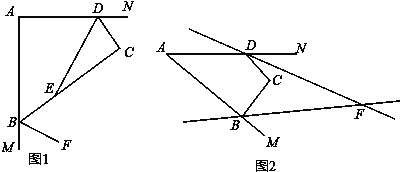
在（1）的条件下，如果正方形CDEF绕点C旋转，连接BE，CE，AF，线段BE与AF的数量关系有无变化？请仅就图2的情形给出证明；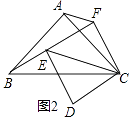

（3）【问题发现】
当正方形CDEF旋转到B，E，F三点共线时候，直接写出线段AF的长．

Answer 1

【答案】
（1）解：在Rt△ABC中，AB=AC=2，

根据勾股定理得，BC= AB=2 ，

点D为BC的中点，

∴AD= BC= ，

∵四边形CDEF是正方形，

∴AF=EF=AD= ，

∵BE=AB=2，

∴BE= AF，

（2）解：无变化；

如图2，在Rt△ABC中，AB=AC=2，

∴∠ABC=∠ACB=45°，

∴sin∠ABC= = ，

在正方形CDEF中，∠FEC= ∠FED=45°，

在Rt△CEF中，sin∠FEC= ，

∴ ，

∵∠FCE=∠ACB=45°，

∴∠FCE﹣∠ACE=∠ACB﹣∠ACE，

∴∠FCA=∠ECB，

∴△ACF∽△BCE，

∴ ，

∴BE= AF，

∴线段BE与AF的数量关系无变化

（3）解：当点E在线段AF上时，如图2，

由（1）知，CF=EF=CD= ，

在Rt△BCF中，CF= ，BC=2 ，

根据勾股定理得，BF= ，

∴BE=BF﹣EF= ﹣ ，

由（2）知，BE= AF，

∴AF= ﹣1，

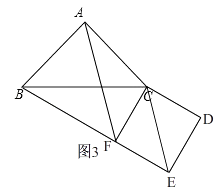
当点E在线段BF的延长线上时，如图3，

在Rt△ABC中，AB=AC=2，

∴∠ABC=∠ACB=45°，

∴sin∠ABC= = ，

在正方形CDEF中，∠FEC= ∠FED=45°，

在Rt△CEF中，sin∠FEC= ，

∴ ，

∵∠FCE=∠ACB=45°，

∴∠FCB+∠ACB=∠FCB+∠FCE，

∴∠FCA=∠ECB，

∴△ACF∽△BCE，

∴ ，

∴BE= AF，

由（1）知，CF=EF=CD= ，

在Rt△BCF中，CF= ，BC=2 ，

根据勾股定理得，BF= ，

∴BE=BF+EF= + ，

由（2）知，BE= AF，

∴AF= +1．

即：当正方形CDEF旋转到B，E，F三点共线时候，线段AF的长为 ﹣1或 +1．

【解析】（1）先利用等腰直角三角形的性质得出AD= ，再得出BE=AB=2，即可得出结论；（2）先利用三角函数得出 ，同理得出 ，夹角相等即可得出△ACF∽△BCE，进而得出结论；（3）分两种情况计算，当点E在线段BF上时，如图2，先利用勾股定理求出EF=CF=AD= ，BF= ，即可得出BE= ﹣ ，借助（2）得出的结论，当点E在线段BF的延长线上，同前一种情况一样即可得出结论．