题目内容
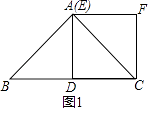
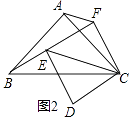
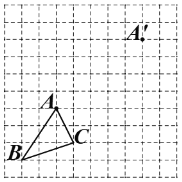
【题目】如图,在边长为1个单位长度的小正方形组成的网格中.
(1)把△ABC平移至![]() 的位置,使点A与
的位置,使点A与![]() 对应,得到△
对应,得到△![]() ;
;
(2)图中可用字母表示,与线段![]() 平行且相等的线有:________;
平行且相等的线有:________;
(3)求四边形![]() 的面积.
的面积.
【答案】(1)见解析;(2)![]() ;(3)14.
;(3)14.
【解析】
(1)根据图形可得,点A向右平移5个单位,向上平移4个单位,分别将B、C按照点A平移的路径进行平移,然后顺次连接;(2)根据平移可得线段AA′与线段CC′相互平行;(3)用四边形ACC′A′所在矩形的面积减去四个小三角形的面积即可得解.
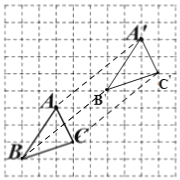
(1)根据图形可得,点A向右平移5个单位,向上平移4个单位,分别将B、C按照点A平移的路径进行平移,然后顺次连接,则△![]() 即为所求.
即为所求.
(2)根据平移可得线段AA′与线段CC′、BB′相互平行且相等,
故答案为:BB′、CC′
(3)S四边形ACC′A′=6×6-(![]() ×4×5+
×4×5+![]() ×2×1)×2=14.
×2×1)×2=14.

【题目】某公司招聘职员,对甲、乙两位候选人进行了面试和笔试,面试中包括形体和口才,笔试中包括专业水平和创新能力考察,他们的成绩(百分制)如下表:
候选人 | 面试 | 笔试 | ||
形体 | 口才 | 专业水平 | 创新能力 | |
甲 | 86 | 90 | 96 | 92 |
乙 | 92 | 88 | 95 | 93 |
若公司根据经营性质和岗位要求认为:形体、口才、专业水平、创新能力按照4:6:5:5的比确定,请计算甲、乙两人各自的平均成绩,看看谁将被录取?
【题目】某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
修造人 | 笔试成绩/分 | 面试成绩/分 |
甲 | 90 | 88 |
乙 | 84 | 92 |
丙 | x | 90 |
丁 | 88 | 86 |
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.