题目内容
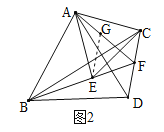
【题目】如图,![]() ,分别以AB、AC为边作等边三角形ABD与等边三角形ACE,连接BE、CD,BE的延长线与CD交于点F,连接AF,有以下四个结论:①
,分别以AB、AC为边作等边三角形ABD与等边三角形ACE,连接BE、CD,BE的延长线与CD交于点F,连接AF,有以下四个结论:①![]() ;②FA平分
;②FA平分![]() ;③
;③![]() ;④
;④![]() .其中一定正确的结论有( )
.其中一定正确的结论有( )
A.1B.2C.3D.4
【答案】C
【解析】
根据等边三角形的性质证出△BAE≌△DAC,可得BE=CD,从而得出①正确;
过A作AM⊥BF于M,过A作AN⊥DC于N,由△BAE≌△DAC得出∠BEA=∠ACD,由等角的补角相等得出∠AEM=∠CAN,由AAS可证△AME≌△ANC,得到AM=AN,由角平分线的判定定理得到FA平分∠EFC,从而得出②正确;
在FA上截取FG,使FG=FE,根据全等三角形的判定与性质得出△AGE≌△CFE,可得AG=CF,即可求得AF=CF+EF,从而得出④正确;
根据CF+EF=AF,CF+DF=CD,得出CD≠AF,从而得出FE≠FD,即可得出③错误.
∵△ABD和△ACE是等边三角形,
∴∠BAD=∠EAC=60°,AE=AC=EC.
∵∠BAE+∠DAE=60°,∠CAD+∠DAE=60°,
∴∠BAE=∠DAC,
在△BAE和△DAC中,
∵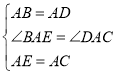 ,
,
∴△BAE≌△DAC(SAS),
∴BE=CD,①正确;
过A作AM⊥BF于M,过A作AN⊥DC于N,如图1.
∵△BAE≌△DAC,
∴∠BEA=∠ACD,
∴∠AEM=∠ACN.
∵AM⊥BF,AN⊥DC,
∴∠AME=∠ANC.
在△AME和△ANC中,∵∠AEM=∠CAN,∠AME=∠ANC,AE=AC,
∴△AME≌△ANC,
∴AM=AN.
∵AM⊥BF,AN⊥DC,AM=AN,FA平分∠EFC,②正确;
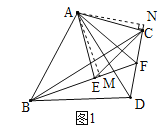
在FA上截取FG,使FG=FE,如图2.
∵∠BEA=∠ACD,∠BEA+∠AEF=180°,
∴∠AEF+∠ACD=180°,
∴∠EAC+∠EFC=180°.
∵∠EAC=60°,
∴∠EFC=120°.
∵FA平分∠EFC,
∴∠EFA=∠CFA=60°.
∵EF=FG,∠EFA=60°,
∴△EFG是等边三角形,
∴EF=EG.
∵∠AEG+∠CEG=60°,∠CEG+∠CEF=60°,
∴∠AEG=∠CEF,
在△AGE和△CFE中,
∵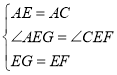 ,
,
∴△AGE≌△CFE(SAS),
∴AG=CF.
∵AF=AG+FG,
∴AF=CF+EF,④正确;
∵CF+EF=AF,CF+DF=CD,CD≠AF,
∴FE≠FD,③错误,
∴正确的结论有3个.
故选C.