题目内容
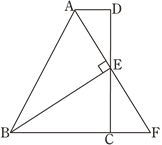
【题目】如图,四边形![]() 内接于⊙
内接于⊙![]() ,
,![]() 是⊙
是⊙![]() 的直径,过点
的直径,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,
,![]() 平分
平分![]() .
.
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)已知![]() cm,
cm,![]() cm,求⊙
cm,求⊙![]() 的半径.
的半径.

【答案】(1)证明见解析;(2)5cm.
【解析】
(1)、根据等边对等角得出∠ODA=∠OAD,进而得出∠OAD=∠EDA,证得EC∥OA,从而证得AE⊥OA,即可证得AE是⊙O的切线;(2)、过点O作OF⊥CD,垂足为点F.从而证得四边形AOFE是矩形,得出OF=AE=4cm,根据垂径定理得出DF=![]() CD=3cm,在Rt△ODF中,根据勾股定理即可求得⊙O的半径.
CD=3cm,在Rt△ODF中,根据勾股定理即可求得⊙O的半径.
(1)、证明:连结OA.∵OA=OD,∴∠ODA=∠OAD.∵DA平分∠BDE,∴∠ODA=∠EDA.
∴∠OAD=∠EDA,∴EC∥OA.∵AE⊥CD,∴OA⊥AE.∵点A在⊙O上,∴AE是⊙O的切线.

(2)、解:过点O作OF⊥CD,垂足为点F.∵∠OAE=∠AED=∠OFD=90°,
∴四边形AOFE是矩形.∴OF=AE=4cm.又∵OF⊥CD,∴DF=![]() CD=3cm.
CD=3cm.
在Rt△ODF中,![]() =5cm, 即⊙O的半径为5cm.
=5cm, 即⊙O的半径为5cm.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目