��Ŀ����
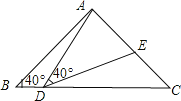
����Ŀ����ͼ���ڡ�ABC�У�AB��AC��2����B����C��40�㣬��D���߶�BC���˶���D����B��C�غϣ�������AD������ADE��40�㣬DE���߶�AC��E��
��1������BDA��115��ʱ����EDC���� ���㣬��DEC���� ���㣻��D��B��C�˶�ʱ����BDA���� �������С������
��2����DC���ڶ���ʱ����ABD�ա�DCE����˵�����ɣ�
��3���ڵ�D���˶������У���ADE����״�����ǵ����������������ԣ���ֱ��д����BDA�Ķ������������ԣ���˵�����ɣ�

���𰸡���1��25�㣬115�㣬С����2����DC��2ʱ����ABD�ա�DCE������������3������BDA�Ķ���Ϊ110���80��ʱ����ADE����״�ǵ��������Σ�������
��������
��1�����ݡ�BDA��115���Լ���ADE��40�㣬���ɵó���EDC��180�㩁��ADB����ADE�����������DEC�Ķ�����
��2����DC��2ʱ�����á�DEC+��EDC��140�㣬��ADB+��EDC��140�㣬�����ADB����DEC��������AB��DC��2�����ɵó���ABD�ա�DCE��
��3������BDA�Ķ���Ϊ110���80��ʱ����ADE����״�ǵ��������Σ�
�⣺��1����EDC��180�㩁��ADB����ADE��180�㩁115�㩁40�㣽25�㣬
��DEC��180�㩁��EDC����C��180�㩁40�㩁25�㣽115�㣬
��BDA����
�ʴ�Ϊ��25�㣬115�㣬С��
��2����DC��2ʱ����ABD�ա�DCE��
���ɣ��ߡ�C��40�㣬
���DEC+��EDC��140�㣬
�֡ߡ�ADE��40�㣬
���ADB+��EDC��140�㣬
���ADB����DEC��
�֡�AB��DC��2��
���ABD�ա�DCE��AAS����
��3������BDA�Ķ���Ϊ110���80��ʱ����ADE����״�ǵ��������Σ�
���ɣ��ߡ�BDA��110��ʱ��
���ADC��70�㣬
�ߡ�C��40�㣬
���DAC��70�㣬��AED����C+��EDC��30��+40�㣽70�㣬
���DAC����AED��
���ADE����״�ǵ��������Σ�
�ߵ���BDA�Ķ���Ϊ80��ʱ��
���ADC��100�㣬
�ߡ�C��40�㣬
���DAC��40�㣬
���DAC����ADE��
���ADE����״�ǵ��������Σ�

 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д� ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�