题目内容
如图,已知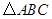 ,以
,以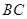 为直径,
为直径,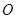 为圆心的半圆交
为圆心的半圆交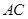 于点
于点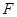 ,点
,点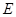 为弧CF的中点,连接
为弧CF的中点,连接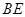 交
交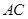 于点
于点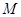 ,
,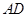 为△ABC的角平分线,且
为△ABC的角平分线,且 ,垂足为点
,垂足为点 .
.
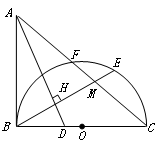
(1)求证: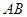 是半圆
是半圆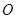 的切线;
的切线;
(2)若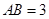 ,
,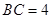 ,求
,求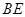 的长.
的长.
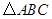 ,以
,以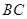 为直径,
为直径,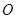 为圆心的半圆交
为圆心的半圆交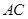 于点
于点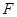 ,点
,点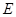 为弧CF的中点,连接
为弧CF的中点,连接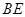 交
交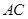 于点
于点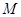 ,
,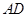 为△ABC的角平分线,且
为△ABC的角平分线,且 ,垂足为点
,垂足为点 .
.
(1)求证:
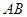 是半圆
是半圆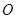 的切线;
的切线;(2)若
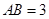 ,
,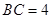 ,求
,求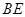 的长.
的长.(1)连结CE,∠BEC=90°,点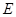 为弧CF的中点,所以∠ECF="∠EBC" , 且
为弧CF的中点,所以∠ECF="∠EBC" , 且
所以AD CE,所以∠ECF="∠MAD=∠EBC,"
CE,所以∠ECF="∠MAD=∠EBC," 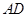 为△ABC的角平分线,得∠MAD="∠BAH=∠EBC," ∠ABH+∠BAH=90°,所以∠ABH+∠EBC =90°,
为△ABC的角平分线,得∠MAD="∠BAH=∠EBC," ∠ABH+∠BAH=90°,所以∠ABH+∠EBC =90°,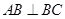
(2)∵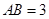 ,
,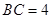 .
.
由(1)知,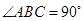 ,∴
,∴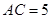 .
.
在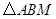 中,
中,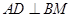 于
于 ,
,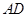 平分
平分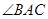 ,
,
∴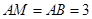 ,∴
,∴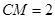 .
.
由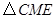 ∽
∽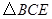 ,得
,得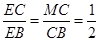 .
.
∴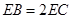 ,
,
∴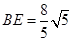 .
.
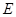 为弧CF的中点,所以∠ECF="∠EBC" , 且
为弧CF的中点,所以∠ECF="∠EBC" , 且
所以AD
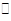 CE,所以∠ECF="∠MAD=∠EBC,"
CE,所以∠ECF="∠MAD=∠EBC," 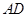 为△ABC的角平分线,得∠MAD="∠BAH=∠EBC," ∠ABH+∠BAH=90°,所以∠ABH+∠EBC =90°,
为△ABC的角平分线,得∠MAD="∠BAH=∠EBC," ∠ABH+∠BAH=90°,所以∠ABH+∠EBC =90°,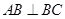
(2)∵
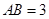 ,
,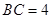 .
.由(1)知,
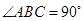 ,∴
,∴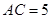 .
.在
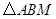 中,
中,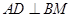 于
于 ,
,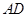 平分
平分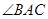 ,
,∴
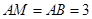 ,∴
,∴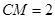 .
.由
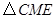 ∽
∽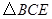 ,得
,得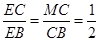 .
.∴
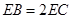 ,
,∴
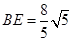 .
.此题考核圆的切线,相似三角形的性质

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

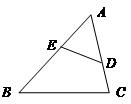

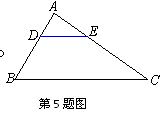
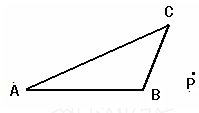
 BC,DE分别交边AB、AC于D、E两点,若△ADE与△ABC的面积比为1:9,则AD:AB的值为 .
BC,DE分别交边AB、AC于D、E两点,若△ADE与△ABC的面积比为1:9,则AD:AB的值为 .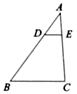
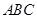 中,
中,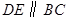 ,
,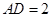 ,
,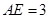 ,
,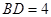 ,则
,则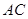 的长为
的长为