题目内容
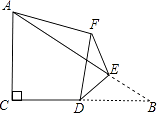
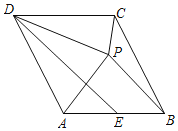
【题目】在菱形ABCD中,![]() ,点E为AB边的中点,点P与点A关于DE对称,连接DP、BP、CP,下列结论:
,点E为AB边的中点,点P与点A关于DE对称,连接DP、BP、CP,下列结论:![]() ;
;![]() ;
;![]() ;
;![]() ,其中正确的是
,其中正确的是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
根据菱形性质和轴对称性质可得AP⊥DE,PA=PB,即DE垂直平分PA,由中垂线性质得,PD=CD,PE=AE,由三角形中线性质得PE=![]() ,得三角形ABP是直角三角形;由等腰三角形性质得,∠DAP=∠DPA, ∠DCP=∠DPC,所以,∠DPA+∠DPC=∠DAP+∠DCP=
,得三角形ABP是直角三角形;由等腰三角形性质得,∠DAP=∠DPA, ∠DCP=∠DPC,所以,∠DPA+∠DPC=∠DAP+∠DCP=![]() .
.
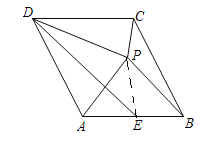
连接PE,
因为,四边形ABCD是菱形,
所以,AB=BC=CD=AD,
因为,点P与点A关于DE对称,
所以,AP⊥DE,PA=PB,即DE垂直平分PA,
所以,PD=CD,PE=AE,
又因为,E是AB的中点,
所以,AE=BE,
所以,PE=![]() ,
,
所以,三角形ABP是直角三角形,
所以,![]() ,
,
所以,![]() .
.
因为DP不在菱形的对角线上,
所以,∠PCD≠30,
又DC=DP,
所以,![]() ,
,
因为,DA=DP=DC,
所以,∠DAP=∠DPA, ∠DCP=∠DPC,
所以,∠DPA+∠DPC=∠DAP+∠DCP=![]() ,
,
即 ![]() .
.
综合上述,正确结论是![]() .
.
故选:B

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
【题目】某旅行社拟在暑假期间面向学生推出“林州红旗渠一日游”活动,收费标准如下:
人数m | 0<m≤100 | 100<m≤200 | m>200 |
收费标准(元/人) | 90 | 85 | 75 |
甲、乙两所学校计划组织本校学生自愿参加此项活动.已知甲校报名参加的学生人数多于100人,乙校报名参加的学生人数少于100人.经核算,若两校分别组团共需花费20 800元,若两校联合组团只需花费18 000元.
(1)两所学校报名参加旅游的学生人数之和超过200人吗?为什么?
(2)两所学校报名参加旅游的学生各有多少人?