题目内容
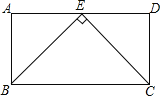
【题目】如图,在矩形ABCD中,E是AD的中点,且![]() 若矩形ABCD的周长为48cm,则矩形ABCD的面积为______
若矩形ABCD的周长为48cm,则矩形ABCD的面积为______![]() .
.
【答案】128
【解析】
根据AB=DC,∠A=∠D,AE=DE,利用SAS可判定△ABE≌△DCE,根据全等三角形的性质可得:∠AEB=∠DEC,再根据BE⊥CE,可得:∠BEC=90°,进而可得:∠AEB=∠DEC=45°,
因此∠EBC=∠ECD=45°,继而可得:AB=AE,DC=DE,即AD=2AB,根据周长=48,可求得:BC=16,AB=8,最后根据矩形面积公式计算可得:S=16×8=128 cm.
∵AB=DC,∠A=∠D,AE=DE,
∴△ABE≌△DCE(SAS),
∴∠AEB=∠DEC,
∵BE⊥CE,
∴∠BEC=90°,
∵∠AEB+∠BEC+∠DEC=180°,
∴∠AEB=∠DEC=45°,
∴∠EBC=∠ECD=45°,
∴AB=AE,DC=DE,
即AD=2AB,
又∵周长=48,
∴BC=16,AB=8,
S=16×8=128 cm,
故答案为:128.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目