题目内容
已知,如图,抛物线y=-x2+bx+c与x轴,y轴分别相交于点A(-1,0),B(0,3)两点,其顶点为D
(1)求该抛物线的解析式;
(2)若抛物线与x轴另一个交点为E,求四边形ABDE的面积.

(1)求该抛物线的解析式;
(2)若抛物线与x轴另一个交点为E,求四边形ABDE的面积.

(1)将点A(-1,0),B(0,3)两点代入解析式可得:
,
解得:
.
故该抛物线的解析式为:y=-x2+2x+3.
(2)由函数解析式为y=-x2+2x+3,可得点D坐标为:(1,4),点E坐标为(3,0),
过点D作DF⊥x轴,交x轴于点F,
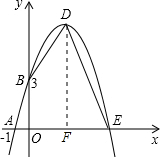
则点F坐标为(1,0),
从而可得S△ABO=
AO×BO=
,
S梯形BOFD=
(BO+DF)×OF=
,S△DFE=
EF×DF=4,
故可得S四边形ABDE=S△ABO+S梯形BOFD+S△DFE=9.
|
解得:
|
故该抛物线的解析式为:y=-x2+2x+3.
(2)由函数解析式为y=-x2+2x+3,可得点D坐标为:(1,4),点E坐标为(3,0),
过点D作DF⊥x轴,交x轴于点F,

则点F坐标为(1,0),
从而可得S△ABO=
| 1 |
| 2 |
| 3 |
| 2 |
S梯形BOFD=
| 1 |
| 2 |
| 7 |
| 2 |
| 1 |
| 2 |
故可得S四边形ABDE=S△ABO+S梯形BOFD+S△DFE=9.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目





 88平方米?
88平方米?