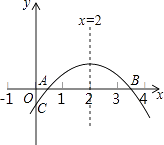题目内容
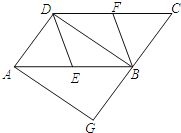
【题目】如图,在平行四边形![]() 中,
中,![]() 分别为边
分别为边![]() 的中点,
的中点,![]() 是对角线,过点
是对角线,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() .
.
(2)若![]() ,
,
①求证:四边形![]() 是菱形.
是菱形.
②当![]() 时,求四边形
时,求四边形![]() 的面积.
的面积.
【答案】(1)见解析;(2)①见解析;②6.
【解析】
(1)由四边形ABCD是平行四边形,可得AB∥CD,AB=CD,又由E、F分别为边AB、CD的中点,易得DF∥BE,DF=BE,即可判定四边形DEBF为平行四边形,则可证得DE∥BF;
(2)①由∠G=90°,AG∥DB,易证得△DBC为直角三角形,又由F为边CD的中点,即可得BF=![]() DC=DF,则可证得:四边形DEBF是菱形;
DC=DF,则可证得:四边形DEBF是菱形;
②根据矩形的判定定理得到四边形AGBD是矩形,根据三角形的面积公式即可得到结论.
证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵E、F分别为AB、CD的中点,
∴DF=![]() DC,BE=
DC,BE=![]() AB,
AB,
∴DF∥BE,DF=BE,
∴四边形DEBF为平行四边形,
∴DE∥BF;
(2)①∵AG∥BD,

∴∠G=∠DBC=90°,
∴△DBC为直角三角形,
又∵F为边CD的中点.
∴BF=![]() DC=DF,
DC=DF,
又∵四边形DEBF为平行四边形,
∴四边形DEBF是菱形;
②∵AD∥BG,AG∥BD,∠G=90°,
∴四边形AGBD是矩形,
∴S△ABD=S△ABG=![]() ×3×4=6,
×3×4=6,
∵E为边AB的中点,
∴S△BDE=![]() S△ABD=3,
S△ABD=3,
∴四边形DEBF的面积=2S△BDE=6.

 阅读快车系列答案
阅读快车系列答案【题目】小楠是一个乐学习,善思考,爱探究的同学,她对函数![]() 的图象和性质进行了探究,请你将下列探究过程补充完整:
的图象和性质进行了探究,请你将下列探究过程补充完整:
(Ⅰ)函数![]() 的自变量x的取值范围是 .
的自变量x的取值范围是 .
(Ⅱ)用描点法画函数图象:
(i)列表:
x | … | ﹣5 | ﹣2 | ﹣1 | 0 | … | 2 | 3 | 4 | 7 | … |
y | … | a | 2 | 3 | b | … | 6 | 3 | 2 | 1 | … |
表中a的值为 ,b的值为 .
(ii)描点连线:请在下图画出该图象的另一部分.
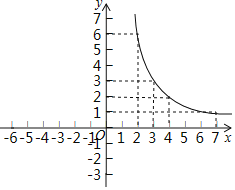
(Ⅲ)观察函数图象,得到函数![]() 的性质:
的性质:
当x 时,函数值y随x的增大而 ;
当x 时,函数值y随x的增大而减少.
(IV)应用:若![]() ≥6,则x的取值范围是 .
≥6,则x的取值范围是 .