题目内容
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,D是AC的中点,E是BC延长线上的一点,且
,D是AC的中点,E是BC延长线上的一点,且![]() ,
,![]() ,垂足为M.
,垂足为M.

![]() 求
求![]() 的度数;
的度数;
![]() 求证:M是BE的中点.
求证:M是BE的中点.
【答案】![]() 30°;(2)见解析.
30°;(2)见解析.
【解析】
(1)先推出△ABC是等边△ABC,再根据等边三角形的性质得到∠ACB=∠ABC=60°,然后根据等边对等角可得:∠E=∠CDE,最后根据外角的性质可求∠E的度数;
(2)连接BD,由等边三角形的三线合一的性质可得:![]() ,结合(1)的结论可得:∠DBC=∠E,然后根据等角对等边,可得:DB=DE,最后根据等腰三角形的三线合一的性质可得:M是BE的中点.
,结合(1)的结论可得:∠DBC=∠E,然后根据等角对等边,可得:DB=DE,最后根据等腰三角形的三线合一的性质可得:M是BE的中点.
(1)解:∵![]() 中,
中,![]() ,
,![]()
∴三角形ABC是等边△ABC,
∴∠ACB=∠ABC=60°,
又∵CE=CD,
∴∠E=∠CDE,
又∵∠ACB=∠E+∠CDE,
∴![]() ;
;
(2)证明:连接BD,
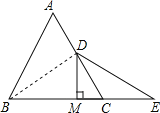
∵等边△ABC中,D是AC的中点,
∴![]()
由(1)知∠E=30°
∴∠DBC=∠E=30°
∴DB=DE
又∵DM⊥BC
∴M是BE的中点.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目