题目内容
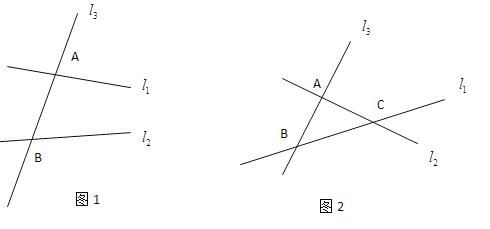
【题目】如图①,在![]() 中,
中,![]() cm ,
cm ,![]() cm,过点
cm,过点![]() 作射线
作射线![]() .点
.点![]() 从点
从点![]() 出发,以3 cm/s的速度沿
出发,以3 cm/s的速度沿![]() 匀速移动;点
匀速移动;点![]() 从点
从点![]() 出发,以
出发,以![]() cm/s的速度沿
cm/s的速度沿![]() 匀速移动.点
匀速移动.点![]() 、
、![]() 同时出发,当点
同时出发,当点![]() 到达点
到达点![]() 时,点
时,点![]() 、
、![]() 同时停止移动.连接
同时停止移动.连接![]() 、
、![]() ,设移动时间为
,设移动时间为![]() (s).
(s).
(1)点![]() 、
、![]() 从移动开始到停止,所用时间为 s;
从移动开始到停止,所用时间为 s;
(2)当![]() 与
与![]() 全等时,
全等时,
①若点![]() 、
、![]() 的移动速度相同,求
的移动速度相同,求![]() 的值;
的值;
②若点![]() 、
、![]() 的移动速度不同,求
的移动速度不同,求![]() 的值;
的值;
(3)如图②,当点![]() 、
、![]() 开始移动时,点
开始移动时,点![]() 同时从点
同时从点![]() 出发,以2 cm/s的速度沿
出发,以2 cm/s的速度沿![]() 向点
向点![]() 匀速移动,到达点
匀速移动,到达点![]() 后立刻以原速度沿
后立刻以原速度沿![]() 返回.当点
返回.当点![]() 到达点
到达点![]() 时,点
时,点![]() 、
、![]() 、
、![]() 同时停止移动.在移动的过程中,是否存在
同时停止移动.在移动的过程中,是否存在![]() 与
与![]() 全等的情形?若存在,求出
全等的情形?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
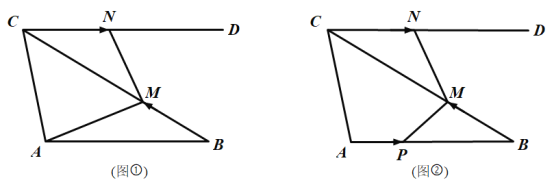
【答案】(1)![]() ;(2)①t=
;(2)①t=![]() ;②a=
;②a=![]() ;(3)t=6.4或t=
;(3)t=6.4或t=![]()
【解析】
(1)根据时间=路程÷速度即可求得答案;
(2)①由题意得:BM=CN=3t,则只可以是△CMN≌△BAM,AB=CM,由此列出方程求解即可;
②由题意得:CN≠BM,则只可以是△CMN≌△BMA,AB=CN=12,CM=BM,进而可得3t=10,求解即可;
(3)分情况讨论,当△CMN≌△BPM时,BP=CM,若此时P由A向B运动,则12-2t=20-3t,但t=8不符合实际,舍去,若此时P由B向A运动,则2t-12=20-3t,求得t=6.4;当△CMN≌△BMP时,则BP=CN,CM=BM,可得3t=10,t=![]() ,再将t=
,再将t=![]() 代入分别求得AP,BP的长及a的值验证即可.
代入分别求得AP,BP的长及a的值验证即可.
解:(1)20÷3=![]() ,
,
故答案为:![]() ;
;
(2)∵CD∥AB,
∴∠B=∠DCB,
∵△CNM与△ABM全等,
∴△CMN≌△BAM或△CMN≌△BMA,
①由题意得:BM=CN=3t,
∴△CMN≌△BAM
∴AB=CM,
∴12=20-3t,
解得:t=![]() ;
;
②由题意得:CN≠BM,
∴△CMN≌△BMA,
∴AB=CN=12,CM=BM,
∴CM=BM=![]() BC,
BC,
∴3t=10,
解得:t=![]()
∵CN=at,
∴![]() a=12
a=12
解得:a=![]() ;
;
(3)存在
∵CD∥AB,
∴∠B=∠DCB,
∵△CNM与△PBM全等,
∴△CMN≌△BPM或△CMN≌△BMP,
当△CMN≌△BPM时,则BP=CM,
若此时P由A向B运动,则BP=12-2t,CM=20-3t,
∵BP=CM,
∴12-2t=20-3t,
解得:t=8 (舍去)
若此时P由B向A运动,则BP=2t-12,CM=20-3t,
∵BP=CM,
∴2t-12=20-3t,
解得:t=6.4,
当△CMN≌△BMP时,则BP=CN,CM=BM,
∴CM=BM=![]() BC
BC
∴3t=10,
解得:t=![]()
当t=![]() 时,点P的路程为AP=2t=
时,点P的路程为AP=2t=![]() ,
,
此时BP=AB-AP=12-![]() =
=![]() ,
,
则CN=BP=![]()
即at=![]() ,
,
∵t=![]() ,
,
∴a=1.6符合题意
综上所述,满足条件的t的值有:t=6.4或t=![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲种节能灯 | 30 | 40 |
甲种节能灯 | 35 | 50 |
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?