Question

【题目】如图 ，已知直线l1，l2，点P在直线l3上且不与点A、B重合．记∠AEP=∠1，∠BFP=∠2，∠EPF=∠3．

（1） 如图 ，若直线l1//l2，点P在线段AB（A、B两点除外）上运动时，写出∠1、∠2、∠3之间的关系，并说明理由．

（2）如图 ，若（1）中∠1、∠2、∠3之间的关系成立，你能不能反向推出直线l1//l2？若成立请说明理由．

（3）如图 ，若直线l1//l2，若点P在A、B两点外侧运动时（不包括线段AB），请直接写出∠1、∠2、∠3之间的关系．

Answer 1

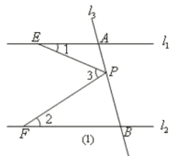
【答案】（1）∠3＝∠1＋∠2，理由见解析．（2）可以反推直线l1//l2.理由见解析.（3）当点P在A点上方时，∠3＝∠2∠1．当点P在B点下方时，∠3＝∠1∠2．

【解析】

（1）过P作直线l1、l2的平行线，利用平行线的性质得到∠1＝∠QPE、∠2＝∠QPF，然后结合这些等角和∠3的位置关系，即可∠1、∠2、∠3的数量关系；

（2）过点P作PQ1平行l1，由PQ1平行l1，得到∠1＝∠Q1PE；又由∠3＝∠Q1PE＋∠Q1PF，且∠3＝∠1＋∠2，得到∠2＝∠QPF，再根据平行线的判定法则进行求解即可得到答案.

（3）本题分两种情况讨论：当点P在A点上方时，过点P作PQ2∥l1∥l2，结合题意可得∠1＝∠Q2PE、∠2＝∠Q2PF；又由∠3＝∠Q2PF∠Q2PE，可得∠3＝∠2∠1．当点P在B点下方时，过点P作PQ3∥l1∥l2，则有图可知：∠1＝∠Q3PE、∠2＝∠Q3PF；根据∠3＝∠Q3PE ∠Q3PF，可得∠3＝∠1∠2．

（1）过P作PQ∥l1∥l2，

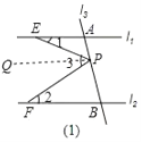
由两直线平行，内错角相等，可得：∠1＝∠QPE、∠2＝∠QPF；
∵∠3＝∠QPE＋∠QPF，
∴∠3＝∠1＋∠2．
（2）可以反推直线l1//l2.理由具体如下：

过点P作PQ1平行l1，如下图（2）所示：

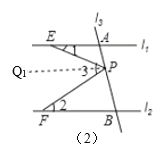
因为PQ1平行l1，所以∠1＝∠Q1PE；又因为∠3＝∠Q1PE＋∠Q1PF，且∠3＝∠1＋∠2，所以可得∠2＝∠QPF，则根据平行线的判定法则：内错角相等，两直线平行可知PQ1平行l2；又由于PQ1平行l1，PQ1平行l2，所以l1//l2.故反推成立.

（3）当点P在A点上方时，过点P作PQ2∥l1∥l2，如下图所示：

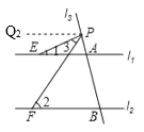
则：∠1＝∠Q2PE、∠2＝∠Q2PF；
∵∠3＝∠Q2PF∠Q2PE，
∴∠3＝∠2∠1．

当点P在B点下方时，过点P作PQ3∥l1∥l2，如下图所示：

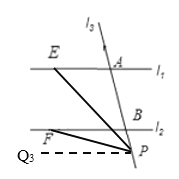
根据题意我们设∠1＝∠PEA、∠2＝∠PFB、∠3＝∠EPF；则有图可知：∠1＝∠Q3PE、∠2＝∠Q3PF；
∵∠3＝∠Q3PE ∠Q3PF，
∴∠3＝∠1∠2．