题目内容
【题目】如图，二次函数y=ax2+bx+c（a≠0）的图象与x轴正半轴相交于A、B两点，与y轴相交于点C，对称轴为直线x=2，且OA=OC，则下列结论：
①abc＞0；②9a+3b+c＜0；③c＞﹣1；④关于x的方程ax2+bx+c=0（a≠0）有一个根为﹣ 
其中正确的结论个数有（ ）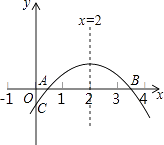
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】解：
由图象开口向下，可知a＜0，
与y轴的交点在x轴的下方，可知c＜0，
又对称轴方程为x=2，所以﹣ 
＞0，所以b＞0，
∴abc＞0，故①正确；
由图象可知当x=3时，y＞0，
∴9a+3b+c＞0，故②错误；
由图象可知OA＜1，
∵OA=OC，
∴OC＜1，即﹣c＜1，
∴c＞﹣1，故③正确；
假设方程的一个根为x=﹣ 
，把x=﹣ 代入方程可得 ﹣ 
+c=0，
整理可得ac﹣b+1=0，
两边同时乘c可得ac2﹣bc+c=0，
即方程有一个根为x=﹣c，
由②可知﹣c=OA，而当x=OA是方程的根，
∴x=﹣c是方程的根，即假设成立，故④正确；
综上可知正确的结论有三个，
故答案为：C．
抛物线开口由a决定，9a+3b+c可由x=3时的函数值看出，由OA=OC可知OA=-c,由图像知ax2+bx+c=0（a≠0）有一个根为-c,由根与系数关系得-c
x2=
,另一个根为
.
练习册系列答案
相关题目
【题目】为了响应市委和市政府“绿色环保，节能减排”的号召，幸福商场用3300元购进甲、乙两种节能灯共计100只，很快售完．这两种节能灯的进价、售价如下表：
进价（元/只） | 售价（元/只） | |
甲种节能灯 | 30 | 40 |
甲种节能灯 | 35 | 50 |
（1）求幸福商场甲、乙两种节能灯各购进了多少只？
（2）全部售完100只节能灯后，商场共计获利多少元？
