Question

【题目】如图，游客在点A处做缆车出发，沿A﹣B﹣D的路线可至山顶D处，假设AB和BD都是直线段，且AB=BD=600m，α=75°，β=45°，求DE的长． （参考数据：sin75°≈0.97，cos75°≈0.26， ≈1.41）

Answer 1

【答案】解：在Rt△ABC中，∵AB=600m，∠ABC=75°， ∴BC=ABcos75°≈600×0.26≈156m，
在Rt△BDF中，∵∠DBF=45°，
∴DF=BDsin45°=600× ≈300×1.41≈423，
∵四边形BCEF是矩形，
∴EF=BC=156，
∴DE=DF+EF=423+156=579m．
答：DE的长为579m．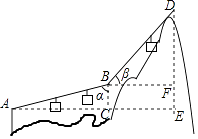

【解析】在R△ABC中，求出BC=ABcos75°≈600×0.26≈156m，在Rt△BDF中，求出DF=BDsin45°=600× ≈300×1.41≈423，由四边形BCEF是矩形，可得EF=BC，由此即可解决问题．