Question

【题目】如图，在一次测量活动中，小丽站在离树底部E处5m的B处仰望树顶C，仰角为30°，已知小丽的眼睛离地面的距离AB为1.65m，那么这棵树大约有多高？（结果精确到0.1m，参考数据： ≈1.73）

Answer 1

【答案】解：过点A作AD⊥CE于点D，如图所示．
∵AB⊥BE，DE⊥BE，AD⊥DE，
∴四边形ABED为矩形，
∴AD=BE=5，DE=AB=1.65．
在Rt△ACD中，AD=5，∠CAD=30°，
∴CD=ADtan∠CAD=5× ≈2.88，
∴CE=CD+DE=2.88+1.65=4.53≈4.5．
答：这棵树大约高4.5米．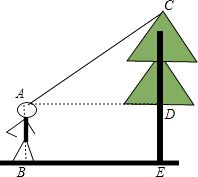

【解析】过点A作AD⊥CE于点D，根据矩形的判定定理证出四边形ABED为矩形，由此即可得出AD=5，DE=1.65，在Rt△ACD中通过解直角三角形以及特殊角的三角函数值即可得出CD的长度，再根据线段间的关系即可得出结论．